Standardized Mean Differences
The calculation of Cohen’s d type effect sizes
Aaron R. Caldwell
2024-07-23
SMD_calcs.RmdThe calculation of standardized mean differences (SMDs) can be helpful in interpreting data and are essential for meta-analysis. In psychology, effect sizes are very often reported as an SMD rather than raw units (though either is fine: see Caldwell and Vigotsky (2020)). In most papers the SMD is reported as Cohen’s d1. The simplest form involves reporting the mean difference (or mean in the case of a one-sample test) divided by the standard deviation.
\[ Cohen's \space d = \frac{Mean}{SD} \]
However, two major problems arise: bias and the calculation of the denominator. First, the Cohen’s d calculation is biased (meaning the effect is inflated), and a bias correction (often referred to as Hedges’ g) is applied to provide an unbiased estimate. Second, the denominator can influence the estimate of the SMD, and there are a multitude of choices for how to calculate the denominator. To make matters worse, the calculation (in most cases an approximation) of the confidence intervals involves the noncentral t distribution. This requires calculating a non-centrality parameter (lambda: \(\lambda\)), degrees of freedom (\(df\)), or even the standard error (sigma: \(\sigma\)) for the SMD. None of these are easy to determine and these calculations are hotly debated in the statistics literature (Cousineau and Goulet-Pelletier 2021).
In this package we originally opted to make the default SMD
confidence intervals as the formulation outlined by Goulet-Pelletier and Cousineau (2018). We found
that that these calculations were simple to implement and provided
fairly accurate coverage for the confidence intervals for any type of
SMD (independent, paired, or one sample). However, even the authors have
outlined some issues with the method in a newer publication (Cousineau and Goulet-Pelletier 2021). Other
packages, such as MOTE (Buchanan et
al. 2019) or effectsize (Ben-Shachar, Lüdecke, and Makowski 2020), use a
simpler formulation of the noncentral t-distribution (nct). The default
option in the package is the nct type of confidence intervals. We have
created an argument for all TOST functions (tsum_TOST and
t_TOST) named smd_ci which allow the user to
specify “goulet” (for the Cousineau and
Goulet-Pelletier (2021) method), “nct” (this will approximately
match the results of Buchanan et al.
(2019) and Ben-Shachar, Lüdecke, and
Makowski (2020)), “t” (central t method), or “z” (normal method).
We would strongly recommend using “nct” or “goulet” for any analysis. It
is important to remember that all of these methods are only
approximations of confidence intervals (of varying degrees of
quality) and therefore should be interpreted with caution.
It is my belief that SMDs provide another interesting description of
the sample, and have very limited inferential utility (though exceptions
apply). You may disagree, and if you are basing your inferences on the
SMD, and the associated confidence intervals, we recommend you go with a
bootstrapping approach (see boot_t_TOST) (Kirby and Gerlanc 2013).
In this section we will detail on the calculations that are involved in calculating the SMD, their associated degrees of freedom, non-centrality parameter, and variance. If these SMDs are being reported in a scientific manuscript, we strongly recommend that the formulas for the SMDs you report be included in the methods section.
Bias Correction (Hedges)
For all SMD calculative approaches the bias correction was calculated as the following:
\[ J = \frac{\Gamma(\frac{df}{2})}{\sqrt{\frac{df}{2}} \cdot \Gamma(\frac{df-1}{2})} \]
The correction factor2 is calculated in R as the following:
J <- exp ( lgamma(df/2) - log(sqrt(df/2)) - lgamma((df-1)/2) )Hedges g (bias corrected Cohen’s d) can then be calculated by multiplying d by J
\[ g = d \cdot J \] When the bias correction is not applied, J is equal to 1.
Independent Samples
For independent samples there are three calculative approaches
supported by TOSTER. One the denominator is the pooled
standard deviation (Cohen’s d), the average standard deviation (Cohen’s
d(av)), and the standard deviation of the control group (Glass’s \(\Delta\)). Currently, the d or d(av) is
selected by whether or not variances are assumed to be equal. If the
variances are not assumed to be equal then Cohen’s d(av) will be
returned, and if variances are assumed to be equal then Cohen’s d is
returned. Glass’s delta can be selected by setting the
glass argument to “glass1” or “glass2”.
Variances Assumed Unequal: Cohen’s d(av)
For this calculation, the denominator is simply the square root of the average variance.
\[ s_{av} = \sqrt \frac {s_{1}^2 + s_{2}^2}{2} \]
The SMD, Cohen’s d(av), is then calculated as the following:
\[ d_{av} = \frac {\bar{x}_1 - \bar{x}_2} {s_{av}} \]
Note: the x with the bar above it (pronounced as “x-bar”) refers the the means of group 1 and 2 respectively.
The degrees of freedom for Cohen’s d(av), derived from Delacre et al. (2021), is the following:
\[ df = \frac{(n_1-1)(n_2-1)(s_1^2+s_2^2)^2}{(n_2-1) \cdot s_1^4+(n_1-1) \cdot s_2^4} \]
The non-centrality parameter (\(\lambda\)) is calculated as the following:
- Under the Cousineau and Goulet-Pelletier
(2021) method (
smd_ci = "goulet"):
\[ \lambda = d_{av} \times \sqrt{\frac{n_1 \cdot n_2(\sigma^2_1+\sigma^2_2)}{2 \cdot (n_2 \cdot \sigma^2_1+n_1 \cdot \sigma^2_2)}} \]
- Under all other methods (nct, t, or z):
\[ \lambda = \frac{2 \cdot (n_2 \cdot \sigma_1^2 + n_1 \cdot \sigma_2^2)} {n_1 \cdot n_2 \cdot (\sigma_1^2 + \sigma_2^2)} \] The standard error (\(\sigma\)) of Cohen’s d(av) is calculated as the following from Bonett (2009)3:
\[ \sigma_{SMD} = \sqrt{d^2 \cdot (\frac{s_1^4}{n_1-1}+\frac{s_2^4}{n_2-1}) \div 8 \cdot s_{av}^4 + (\frac{s_1^2}{n_1-1}+\frac{s_2^2}{n_2-1}) \div s_{av}^2} \]
Variances Assumed Equal: Cohen’s d
For this calculation, the denominator is simply the pooled standard deviation.
\[ s_{p} = \sqrt \frac {(n_{1} - 1)s_{1}^2 + (n_{2} - 1)s_{2}^2}{n_{1} + n_{2} - 2} \]
\[ d = \frac {\bar{x}_1 - \bar{x}_2} {s_{p}} \]
The degrees of freedom for Cohen’s d is the following:
\[ df = n_1 + n_2 - 2 \]
The non-centrality parameter (\(\lambda\)) is calculated as the following:
- Under the Cousineau and Goulet-Pelletier
(2021) method (
smd_ci = "goulet"):
\[ \lambda = d \cdot \sqrt \frac{\tilde n}{2} \]
wherein, \(\tilde n\) is the harmonic mean of the 2 sample sizes which is calculated as the following:
\[ \tilde n = \frac{2 \cdot n_1 \cdot n_2}{n_1 + n_2} \]
- Under all other methods (nct, t, or z):
\[ \lambda = \frac{1}{n_1} +\frac{1}{n_2} \]
The standard error (\(\sigma\)) of Cohen’s d is calculated as the following:
- Under the Cousineau and Goulet-Pelletier
(2021) method (
smd_ci = "goulet"):
\[ \sigma_{SMD} = \sqrt{\frac{df}{df-2} \cdot \frac{2}{\tilde n} (1+d^2 \cdot \frac{\tilde n}{2}) -\frac{d^2}{J}} \]
- Under all other methods (nct, t, or z) it is calculated using the “unbiased” estimate from Viechtbauer (2007) (table 1; equation 26)4:
\[ \sigma_{SMD} = \sqrt{\frac{1}{n_1} + \frac{1}{n_2} + (1 - \frac{df-2}{df \cdot J^2}) \cdot d_s^2} \]
Glass’s Delta
For this calculation, the denominator is simply the standard
deviation of one of the groups (x for
glass = "glass1", or y for
glass = "glass2".
\[ s_{c} = SD_{control \space group} \]
\[ d = \frac {\bar{x}_1 - \bar{x}_2} {s_{c}} \]
The degrees of freedom for Glass’s delta is the following:
\[ df = n_c - 1 \]
The non-centrality parameter (\(\lambda\)) is calculated as the following:
- Under the Cousineau and Goulet-Pelletier
(2021) method (
smd_ci = "goulet"):
\[ \lambda = d \cdot \sqrt \frac{\tilde n}{2} \]
wherein, \(\tilde n\) is the harmonic mean of the 2 sample sizes which is calculated as the following:
\[ \tilde n = \frac{2 \cdot n_1 \cdot n_2}{n_1 + n_2} \]
- Under all other methods (nct, t, or z):
\[ \lambda = \frac{1}{n_T} + \frac{s_c^2}{n_c \cdot s_c^2} \]
The standard error (\(\sigma\)) of Glass’s delta is calculated as the following:
- Under the Cousineau and Goulet-Pelletier
(2021) method (
smd_ci = "goulet"):
\[ \sigma_{SMD} = \sqrt{\frac{df}{df-2} \cdot \frac{2}{\tilde n} (1+d^2 \cdot \frac{\tilde n}{2}) -\frac{d^2}{J}} \]
- Under all other methods5 (nct, t, or z) derived from Bonett (2008):
\[ \sigma_{SMD} = \sqrt{\frac{s_e^2 \div s_c^2}{n_e-1}+ \frac{1}{n_c-1}+ \frac{d^2}{2 \cdot (n_c-1)}} \]
Paired Samples
For paired samples there are two calculative approaches supported by
TOSTER. One the denominator is the standard deviation of
the change score (Cohen’s d(z)), the correlation corrected effect size
(Cohen’s d(rm)), and the standard deviation of the control condition
(Glass’s \(\Delta\)). Currently, the
choice is made by the function based on whether or not the user sets
rm_correction to TRUE. If rm_correction is set
to t TRUE then Cohen’s d(rm) will be returned, and otherwise Cohen’s
d(z) is returned. This can be overridden and Glass’s delta is returned
if the glass argument is set to “glass1” or “glass2”.
Cohen’s d(z): Change Scores
For this calculation, the denominator is the standard deviation of the difference scores which can be calculated from the standard deviations of the samples and the correlation between the paired samples.
\[ s_{diff} = \sqrt{sd_1^2 + sd_2^2 - 2 \cdot r_{12} \cdot sd_1 \cdot sd_2} \]
The SMD, Cohen’s d(z), is then calculated as the following:
\[ d_{z} = \frac {\bar{x}_1 - \bar{x}_2} {s_{diff}} \]
The degrees of freedom for Cohen’s d(z) is the following:
- Under the Cousineau and Goulet-Pelletier
(2021) method (
smd_ci = "goulet"):
\[ df = 2 \cdot (N_{pairs}-1) \]
- Under all other methods (nct, t, or z):
\[ df = N - 1 \]
The non-centrality parameter (\(\lambda\)) is calculated as the following:
- Under the Cousineau and Goulet-Pelletier
(2021) method (
smd_ci = "goulet"):
\[ \lambda = d_{z} \cdot \sqrt \frac{N_{pairs}}{2 \cdot (1-r_{12})} \]
- Under all other methods (nct, t, or z):
\[ \lambda = \frac{1}{n} \]
The standard error (\(\sigma\)) of Cohen’s d(z) is calculated as the following:
- Under the Cousineau and Goulet-Pelletier
(2021) method (
smd_ci = "goulet"):
\[ \sigma_{SMD} = \sqrt{\frac{df}{df-2} \cdot \frac{2 \cdot (1-r_{12})}{n} \cdot (1+d^2 \cdot \frac{n}{2 \cdot (1-r_{12})}) -\frac{d^2}{J^2}} \space \times \space \sqrt {2 \cdot (1-r_{12})} \]
- Under all other methods (nct, t, or z) it calculated using the “unbiased” estimate from Viechtbauer (2007) (table 1; equation 26)6:
\[ \sigma_{SMD} = \sqrt{\frac{1}{N} + (1 - \frac{df-2}{df \cdot J^2}) \cdot d_z^2} \]
Cohen’s d(rm): Correlation Corrected
For this calculation, the same values for the same calculations above is adjusted for the correlation between measures. As Goulet-Pelletier and Cousineau (2018) mention, this is useful for when effect sizes are being compared for studies that involve between and within subjects designs.
First, the standard deviation of the difference scores are calculated
\[ s_{diff} = \sqrt{sd_1^2 + sd_2^2 - 2 \cdot r_{12} \cdot sd_1 \cdot sd_2} \]
The SMD, Cohen’s d(rm), is then calculated with a small change to the denominator7:
\[ d_{rm} = \frac {\bar{x}_1 - \bar{x}_2}{s_{diff}} \cdot \sqrt {2 \cdot (1-r_{12})} \]
The degrees of freedom for Cohen’s d(rm) is the following:
- Under the Cousineau and Goulet-Pelletier
(2021) method (
smd_ci = "goulet"):
\[ df = 2 \cdot (N_{pairs}-1) \]
- Under all other methods (nct, t, or z):
\[ df = N - 1 \]
The non-centrality parameter (\(\lambda\)) is calculated as the following:
- Under the Cousineau and Goulet-Pelletier
(2021) method (
smd_ci = "goulet"):
\[ \lambda = d_{rm} \cdot \sqrt \frac{N_{pairs}}{2 \cdot (1-r_{12})} \]
- Under all other methods (nct, t, or z):
\[ \lambda = \frac{1}{n} \]
The standard error (\(\sigma\)) of Cohen’s d(rm) is calculated as the following:
\[ \sigma_{SMD} = \sqrt{\frac{df}{df-2} \cdot \frac{2 \cdot (1-r_{12})}{n} \cdot (1+d_{rm}^2 \cdot \frac{n}{2 \cdot (1-r_{12})}) -\frac{d_{rm}^2}{J^2}} \]
Glass’s Delta
For this calculation, the denominator is simply the standard
deviation of one of the groups (x for
glass = "glass1", or y for
glass = "glass2".
\[ s_{c} = SD_{control \space condition} \]
\[ d = \frac {\bar{x}_1 - \bar{x}_2} {s_{c}} \]
The degrees of freedom for Glass’s delta is the following:
- Under the Cousineau and Goulet-Pelletier
(2021) method (
smd_ci = "goulet"):
\[ df = 2 \cdot N - 1 \]
- Under all other methods (nct, t, or z):
\[ df = N - 1 \]
The non-centrality parameter (\(\lambda\)) is calculated as the following:
- Under the Cousineau and Goulet-Pelletier
(2021) method (
smd_ci = "goulet"):
\[ \lambda = d \cdot \sqrt{\frac{N}{2 \cdot (1 - r_{12})}} \]
- Under all other methods (nct, t, or z):
\[ \lambda = \frac{1}{N} \]
The standard error (\(\sigma\)) of Glass’s delta is calculated as the following derived8 from Bonett (2008):
\[ \sigma_{SMD} = \sqrt{\frac{s_{diff}^2}{s_c^2 \cdot df} + \frac{d^2}{2 \cdot df}} \]
One Sample
For a one-sample situation, the calculations are very straight forward
For this calculation, the denominator is simply the standard deviation of the sample.
\[ s={\sqrt {{\frac {1}{N-1}}\sum _{i=1}^{N}\left(x_{i}-{\bar {x}}\right)^{2}}} \]
The SMD is then the mean of X divided by the standard deviation.
\[ d = \frac {\bar{x}} {s} \]
The degrees of freedom for Cohen’s d is the following:
\[ df = N - 1 \]
The non-centrality parameter (\(\lambda\)) is calculated as the following:
\[ \lambda = d \cdot \sqrt N \]
The standard error (\(\sigma\)) of Cohen’s d is calculated as the following:
- Under the Cousineau and Goulet-Pelletier
(2021) method (
smd_ci = "goulet"):
\[ \sigma_{SMD} = \sqrt{\frac{df}{df-2} \cdot \frac{1}{N} (1+d^2 \cdot N) -\frac{d^2}{J^2}} \]
- Under all other methods (nct, t, or z):
\[ \sigma_{SMD} = \sqrt{\frac{1}{n} + \frac{d^2}{(2 \cdot n)}} \]
Confidence Intervals
For the SMDs calculated in this package we use the non-central t method, those outlined by Goulet-Pelletier and Cousineau (2018), and approximate methods using the t and normal distributions. These calculations are only approximations and newer formulations may provide better coverage (e.g., Cousineau and Goulet-Pelletier 2021). In any case, if the calculation of confidence intervals for SMDs is of the utmost importance then I would strongly recommend using bootstrapping techniques rather than any of these approximations whenever possible (Kirby and Gerlanc 2013).
The calculations of the confidence intervals for the
goulet and nct methods involve a two step
process: 1) using the noncentral t-distribution to calculate
the lower and upper bounds of \(\lambda\), and 2) transforming this back to
the effect size estimate. These noncentrality methods are not without
their detractors (Spanos 2021). The normal
and t methods are much simpler and less computationally
intensive, but may have varying levels of accuracy (see Viechtbauer 2007 for more details).
Cousineau and Goulet-Pelletier (2021) Method (smd_ci = “goulet”)
Calculate confidence intervals around \(\lambda\).
\[ t_L = t_{(1/2-(1-\alpha)/2,\space df, \space \lambda)} \\ t_U = t_{(1/2+(1-\alpha)/2,\space df, \space \lambda)} \]
Then transform back to the SMD.
\[ d_L = \frac{t_L}{\lambda} \cdot d \\ d_U = \frac{t_U}{\lambda} \cdot d \]
The non-central t-method (smd_ci = “nct”)
This method is commonly reported in the literature and in other R
packages (e.g., effectsize). However, it is not without
criticism (Spanos 2021; Viechtbauer
2007).
In thise method, you calculate the non-centrality parameters necessary to form confidence intervals wherein the observed t-statistic (\(t_{obs}\))is utilized.
\[ t_L = t_{(1-alpha,\space df, \space t_{obs})} \\ t_U = t_{(alpha,\space df, \space t_{obs})} \] The confidence intervals can then be constructed using the non-centrality parameter and the bias correction.
\[ d_L = t_L \cdot \sqrt{\lambda} \cdot J \\ d_U = t_U \cdot \sqrt{\lambda} \cdot J \]
Central t-method
This is less commonly used though it might perform alright in some scenarios, and as Bonett (2008) and Viechtbauer (2007) report it might perform adequately under with an adequately large sample size.
The limits of the t-distribution at the given alpha-level and degrees
of freedom (qt(1-alpha,df)) are multiplied by the standard
error of the calculated SMD.
\[ CI = SMD \space \pm \space t_{(1-\alpha,df)} \cdot \sigma_{SMD} \]
Normal method
This method will often be the most liberal estimate for the confidence interval. But as Bonett (2008) and Viechtbauer (2007) report, it might perform adequately under with an adequately large sample size. The use of the normal distribution can be justified by the fact that SMDs are asympototically normal.
The limits of the z-distribution at the given alpha-level
(qnorm(1-alpha)) are multiplied by the standard error of
the calculated SMD.
\[ CI = SMD \space \pm \space z_{(1-\alpha)} \cdot \sigma_{SMD} \]
Just Estimate the SMD
It was requested that a function be provided that only calculates the
SMD. Therefore, I created the smd_calc and
boot_smd_calc functions9. The interface is almost the same as
t_TOST but you don’t set an equivalence bound.
smd_calc(formula = extra ~ group,
data = sleep,
paired = TRUE,
smd_ci = "nct",
bias_correction = F)
#> estimate SE lower.ci upper.ci conf.level
#> Cohen's d(z) -1.284558 0.6831444 -2.118017 -0.4146278 0.95
# Setting bootstrap replications low to
## reduce compiling time of vignette
boot_smd_calc(formula = extra ~ group,
data = sleep,
R = 199,
paired = TRUE,
boot_ci = "stud",
bias_correction = F)
#> estimate bias SE lower.ci upper.ci conf.level
#> Cohen's d(z) -1.284558 0.1227613 0.6987096 -1.660945 1.848945 0.95
#> boot_ci
#> Cohen's d(z) studPlotting SMDs
Sometimes you may take a different approach to calculating the SMD,
or you may only have the summary statistics from another study. For this
reason, I have included a way to plot the SMD based on just three
values: the estimate of the SMD, the degrees of freedom, and the
non-centrality parameter/standard error. So long as all three are
reported, or can be estimated, then a plot of the SMD can be produced.
The non-centrality parameter is needed if you want to plot the estimates
using the "goulet" method while the standard error is
needed if you want to plot the z (normal) or t
(t-distribution) methods.
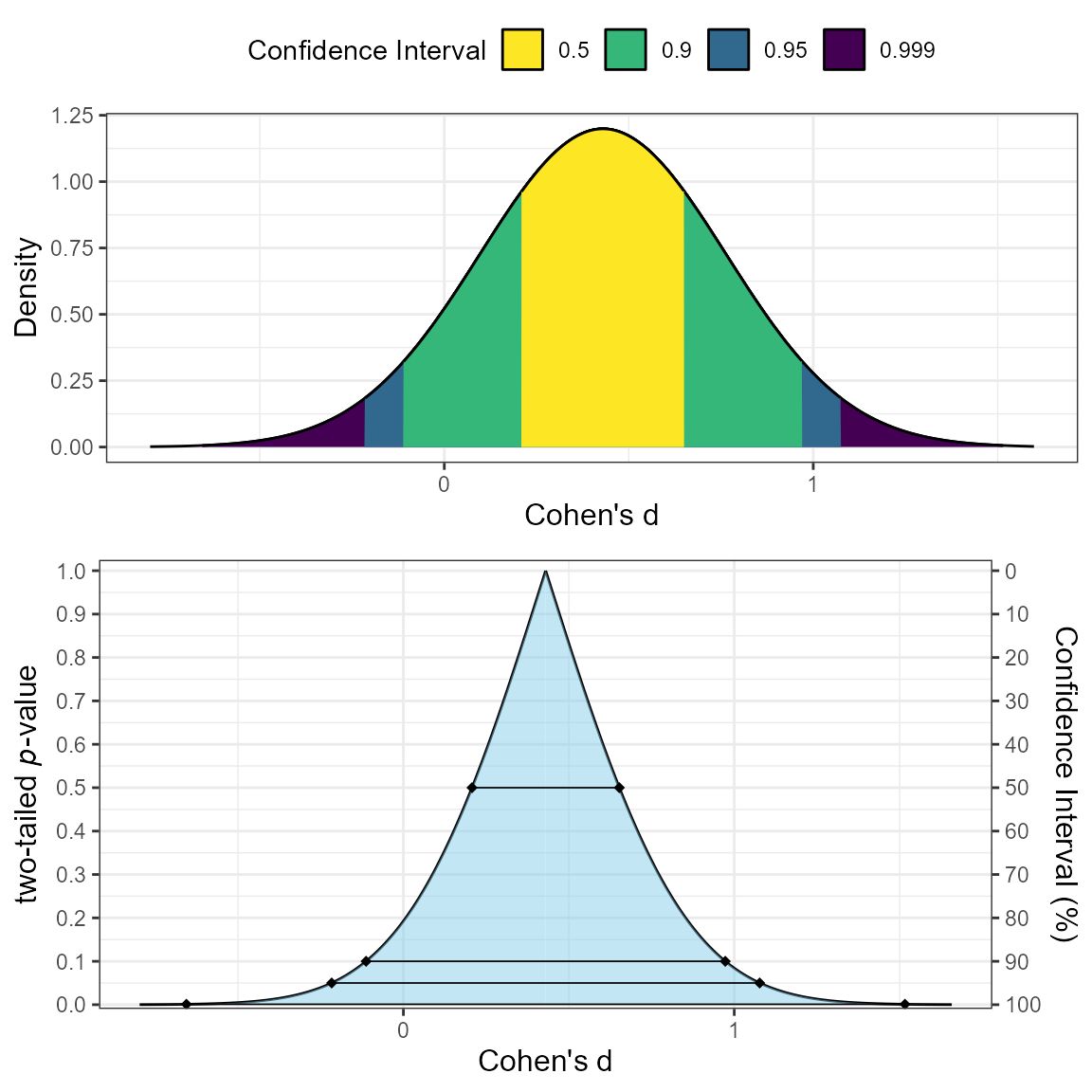
Two types of plots can be produced: consonance
(type = "c"), consonance density
(type = "cd"), or both (the default option;
(type = c("c","cd")))
plot_smd(d = .43,
df = 58,
sigma = .33,
smd_label = "Cohen's d",
smd_ci = "z"
)
Comparing SMDs
In some cases, the SMDs between original and replication studies want to be compared. Rather than looking at whether or not a replication attempt is significant, a researcher could compare to see how compatible the SMDs are between the two studies.
For example, say there is original study reports an effect of Cohen’s dz = 0.95 in a paired samples design with 25 subjects. However, a replication doubled the sample size, found a non-significant effect at an SMD of 0.2. Are these two studies compatible? Or, to put it another way, should the replication be considered a failure to replicate?
We can use the compare_smd function to at least measure
how often we would expect a discrepancy between the original and
replication study if the same underlying effect was being measured (also
assuming no publication bias or differences in protocol).
We can see from the results below that, if the null hypothesis were true, we would only expect to see a discrepancy in SMDs between studies, at least this large, ~1% of the time.
compare_smd(smd1 = 0.95,
n1 = 25,
smd2 = 0.23,
n2 = 50,
paired = TRUE)
#>
#> Difference in Cohen's dz (paired)
#>
#> data: Summary Statistics
#> z = 2.5685, p-value = 0.01021
#> alternative hypothesis: true difference in SMDs is not equal to 0
#> sample estimates:
#> difference in SMDs
#> 0.72Raw Data
The above results are only based on an approximating the differences
between the SMDs. If the raw data is available, then the optimal
solution is the bootstrap the results. This can be accomplished with the
boot_compare_smd function.
For this example, we will simulate some data.
set.seed(4522)
diff_study1 = rnorm(25,.95)
diff_study2 = rnorm(50)
boot_test = boot_compare_smd(x1 = diff_study1,
x2 = diff_study2,
paired = TRUE)
boot_test
#>
#> Bootstrapped Differences in SMDs (paired)
#>
#> data: Bootstrapped
#> z (observed) = 2.887, p-value = 0.006003
#> alternative hypothesis: true difference in SMDs is not equal to 0
#> 95 percent confidence interval:
#> 0.3161207 1.4831351
#> sample estimates:
#> difference in SMDs
#> 0.8058872
# Table of bootstrapped CIs
knitr::kable(boot_test$df_ci, digits = 4)| estimate | lower.ci | upper.ci | |
|---|---|---|---|
| Difference in SMD | 0.8059 | 0.3161 | 1.4831 |
| SMD1 | 0.9418 | 0.5403 | 1.5318 |
| SMD2 | 0.1359 | -0.1420 | 0.4187 |
Visualize
The results of the bootstrapping are stored in the results. So we can even visualize the differences in SMDs.
library(ggplot2)
list_res = boot_test$boot_res
df1 = data.frame(study = c(rep("original",length(list_res$smd1)),
rep("replication",length(list_res$smd2))),
smd = c(list_res$smd1,list_res$smd2))
ggplot(df1,
aes(fill = study, color =smd, x = smd))+
geom_histogram(aes(y=..density..), alpha=0.5,
position="identity")+
geom_density(alpha=.2) +
labs(y = "", x = "SMD (bootstrapped estimates)") +
theme_classic()
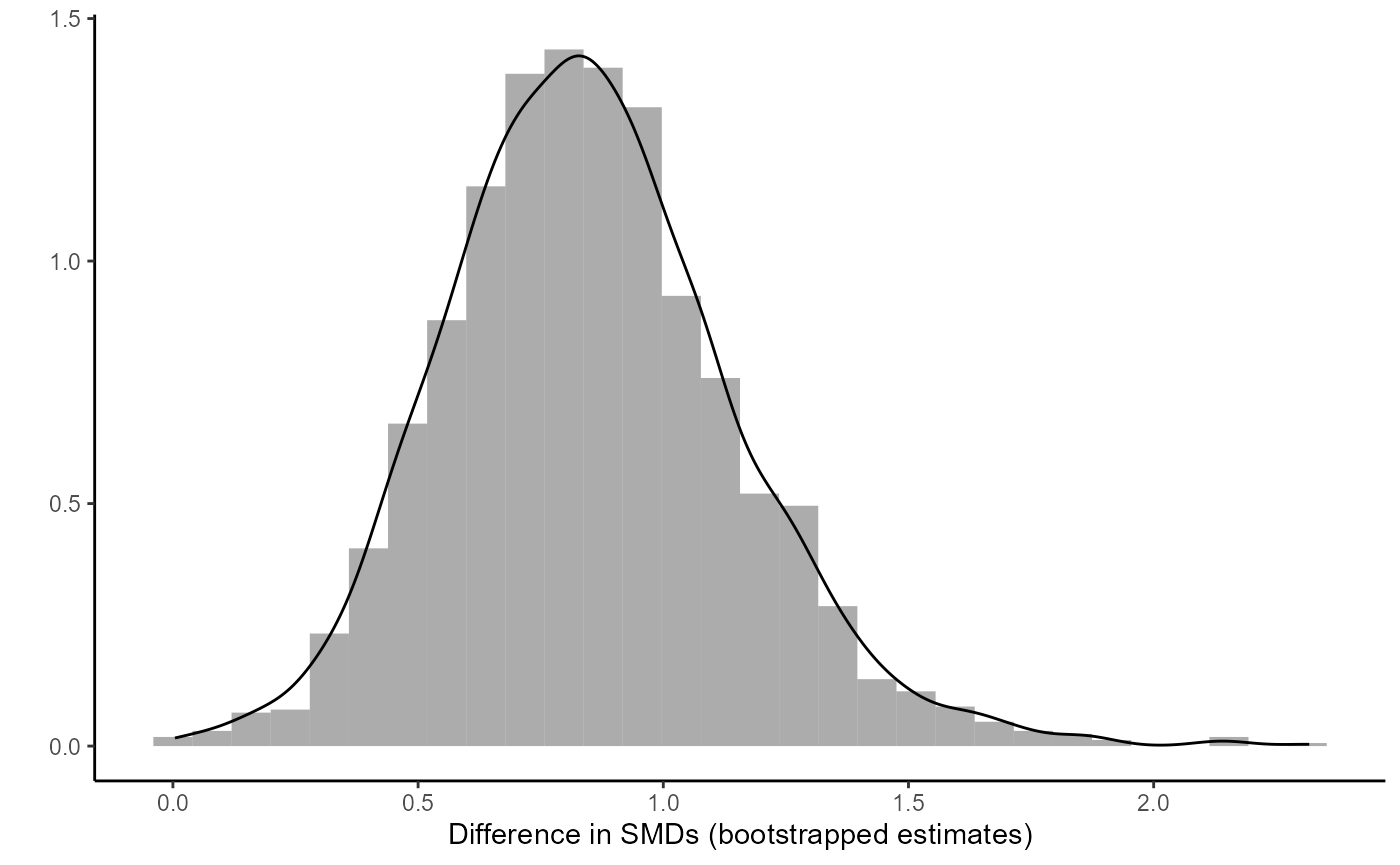
#> `stat_bin()` using `bins = 30`. Pick better value with `binw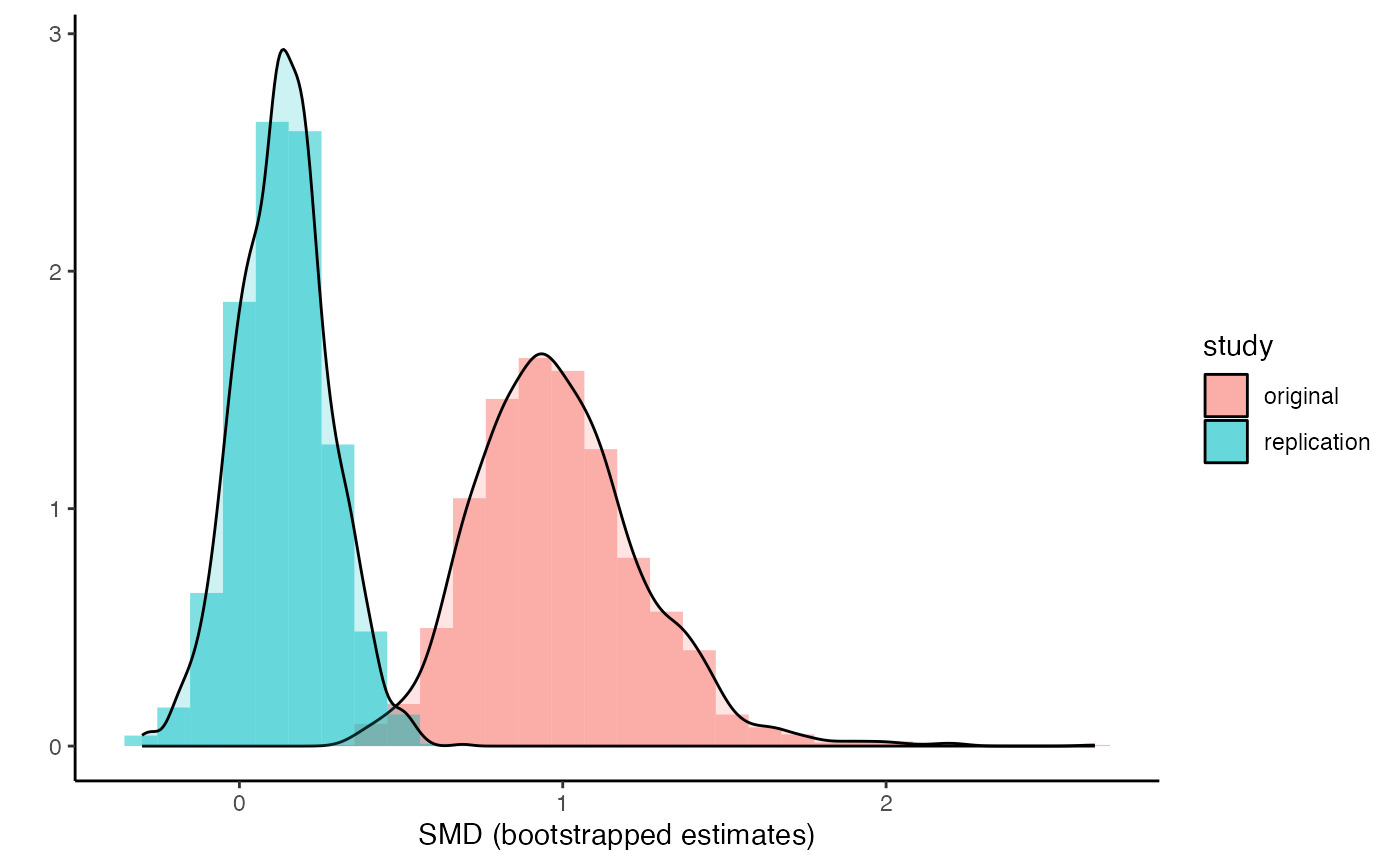idth`.
df2 = data.frame(diff = list_res$d_diff)
ggplot(df2,
aes(x = diff))+
geom_histogram(aes(y=..density..), alpha=0.5,
position="identity")+
geom_density(alpha=.2) +
labs(y = "", x = "Difference in SMDs (bootstrapped estimates)") +
theme_classic()
#> `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
References
I’d argue it is more appropriate to label it as a SMD since many times researchers are not reporting Jacob Cohen’s original formulation. Therefore it is more accurate descriptor to label any SMD as SMD↩︎
This calculation was derived from the supplementary material of Cousineau and Goulet-Pelletier (2021).↩︎
This changed from the original formulation, I believe the current version is a better estimate↩︎
This assumes degrees of freedom of N-2↩︎
Originally, I used an estimate of the standard error from Morris and DeShon. However, it was pointed out by colleague that this wasn’t very accurate. We now use what is used in the metafor R package for the “SMD1H” which is the use of one sample SD as the denominator under the assumption of heterogeneous variances↩︎
This assumes degrees of freedom of N-1↩︎
This is incorrectly stated in the article by Goulet-Pelletier and Cousineau (2018); the correct notation is provided by Lakens (2013)↩︎
Originally, Borenstein et al. (2021) was utilized for this SE calculation. However, upon finding the estimate from Bonett (2008), which is utilized in the
metaforR package for heterogenous variance estimates, we have opted to use this estimate instead.↩︎The results differ greatly because the bootstrap CI method, studentized, is more conservative than the parametric method. This difference is more apparent with extremely small samples like that in the
sleepdataset.↩︎