Plot Distribution of Standardized Mean Difference (SMD)
plot_smd.RdCreates consonance plots (confidence curves and/or consonance density functions) for standardized mean differences (SMDs), allowing visualization of uncertainty around effect size estimates.
Arguments
- d
Estimate of the standardized mean difference (Cohen's d, Hedges' g, etc.).
- df
Degrees of freedom for the standardized mean difference.
- lambda
The non-centrality parameter for the standardized mean difference. Required when
smd_ci = "goulet".- sigma
The standard error for the standardized mean difference. Required when
smd_ciis "t" or "z".- smd_ci
Method for calculating SMD confidence intervals:
"t": central t-distribution method
"z": normal distribution method
"goulet": Goulet-Pelletier method
"nct": noncentral t-distribution method (not currently supported)
- smd_label
Label for the x-axis indicating the SMD measure (default: "SMD"). Common labels include "Cohen's d", "Hedges' g", or "Glass's delta".
- type
Choose which plot(s) to create:
"c": consonance function only (p-values across potential parameter values)
"cd": consonance density function only (distribution of plausible parameter values)
c("c", "cd"): both plots together (default)
- levels
Numeric vector of confidence levels to display (default: c(.5, .9, .95, .999)). These correspond to the confidence intervals shown on the plot.
Details
Consonance plots provide a graphical representation of the full range of confidence intervals for standardized mean differences at different confidence levels. These plots help visualize the uncertainty around effect size estimates and go beyond the traditional approach of reporting only a single confidence interval (typically 95%).
The function creates two types of visualizations:
Consonance function ("c"): Shows how p-values change across different possible values of the SMD. The x-axis represents possible parameter values, and the y-axis represents the corresponding p-values from two-sided hypothesis tests.
Consonance density ("cd"): Shows the distribution of plausible values for the SMD. This can be interpreted as showing where the "weight of evidence" is concentrated.
This function requires specific input parameters depending on the chosen confidence interval method:
For "goulet" method:
d,df, andlambdamust be providedFor "t" and "z" methods:
d,df, andsigmamust be providedThe "nct" method is not currently supported
The required parameters can typically be extracted from the results of functions like
t_TOST(), smd_calc(), or from the smd component of these function results.
These plots are particularly useful for:
Visualizing uncertainty around SMD estimates
Understanding the precision of effect size estimates
Comparing the relative plausibility of different effect sizes
Going beyond the binary "significant vs. non-significant" interpretation
These types of plots are discussed by Schweder & Hjort (2016) and Rafi & Greenland (2020).
References
Schweder, T., & Hjort, N. L. (2016). Confidence, likelihood, probability: Statistical inference with confidence distributions. Cambridge University Press. ISBN: 9781316445051
Rafi, Z., & Greenland, S. (2020). Semantic and cognitive tools to aid statistical science: Replace confidence and significance by compatibility and surprise. BMC Medical Research Methodology, 20, 244. doi:10.1186/s12874-020-01105-9
Examples
# Example 1: Basic consonance plot for Cohen's d using z-method
plot_smd(d = 0.5, df = 40, sigma = 0.164, smd_ci = "z", smd_label = "Cohen's d")
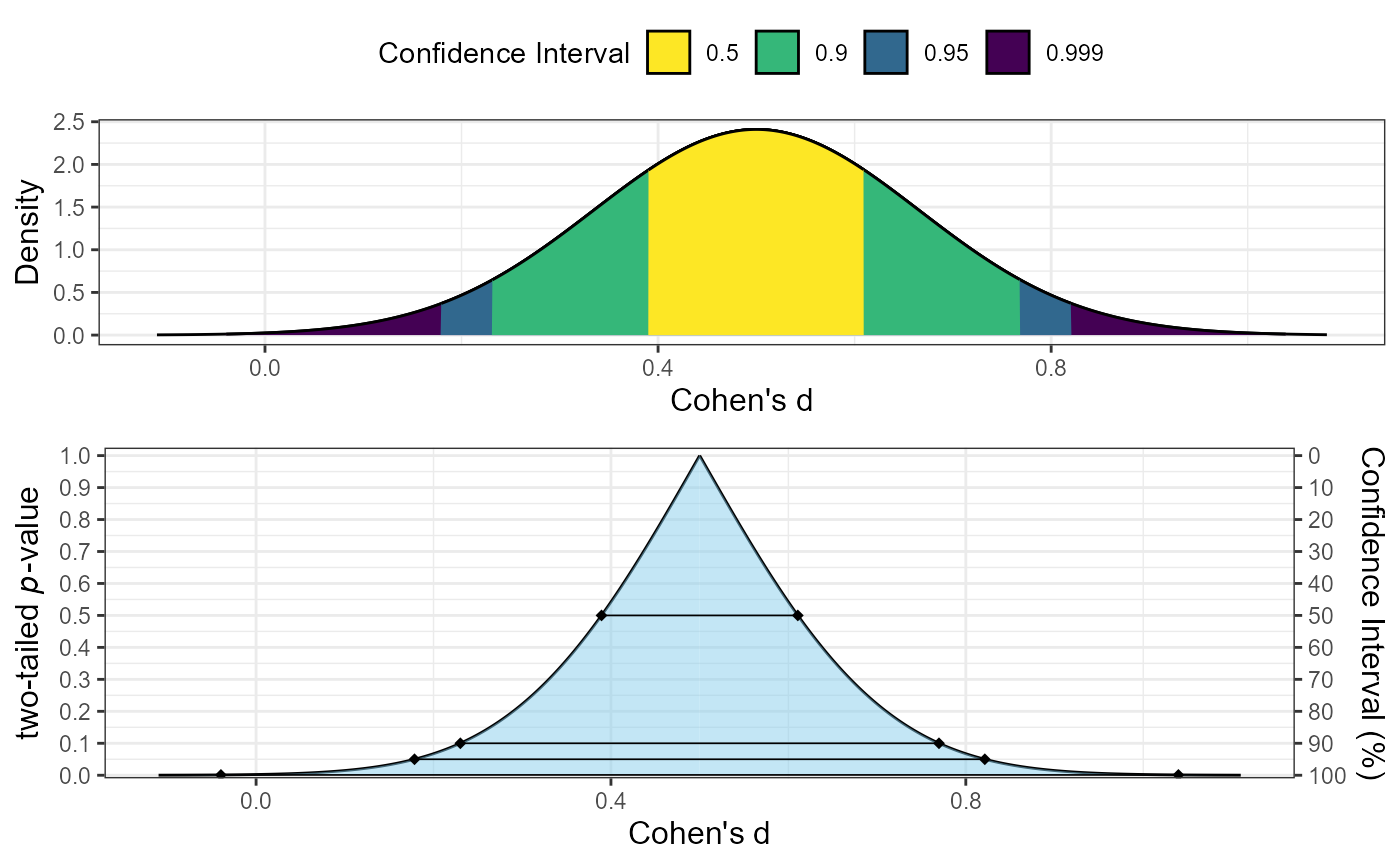 # Example 2: Consonance function only for Hedges' g using t-method
plot_smd(d = 0.45, df = 28, sigma = 0.192, smd_ci = "t",
smd_label = "Hedges' g", type = "c")
# Example 2: Consonance function only for Hedges' g using t-method
plot_smd(d = 0.45, df = 28, sigma = 0.192, smd_ci = "t",
smd_label = "Hedges' g", type = "c")
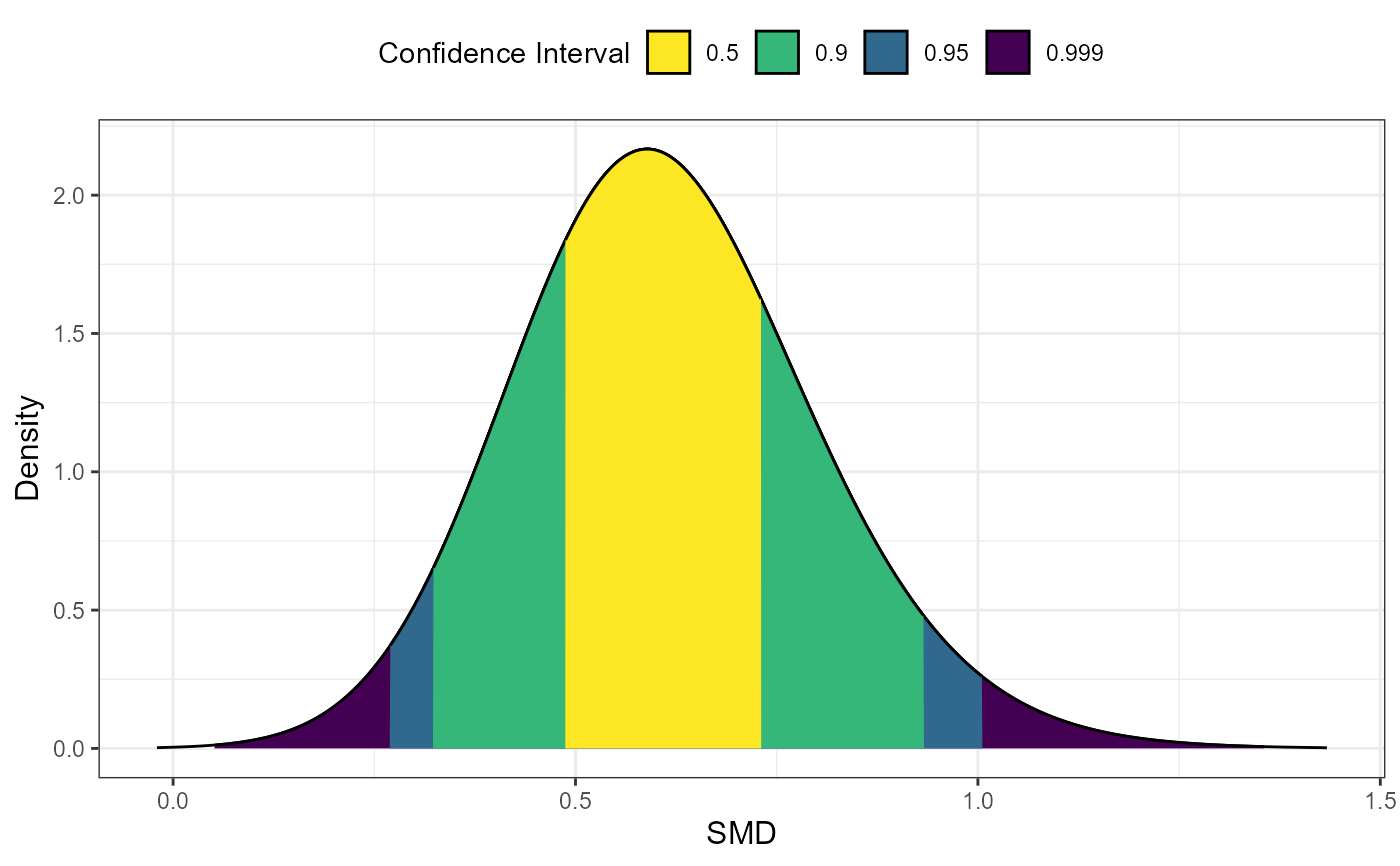
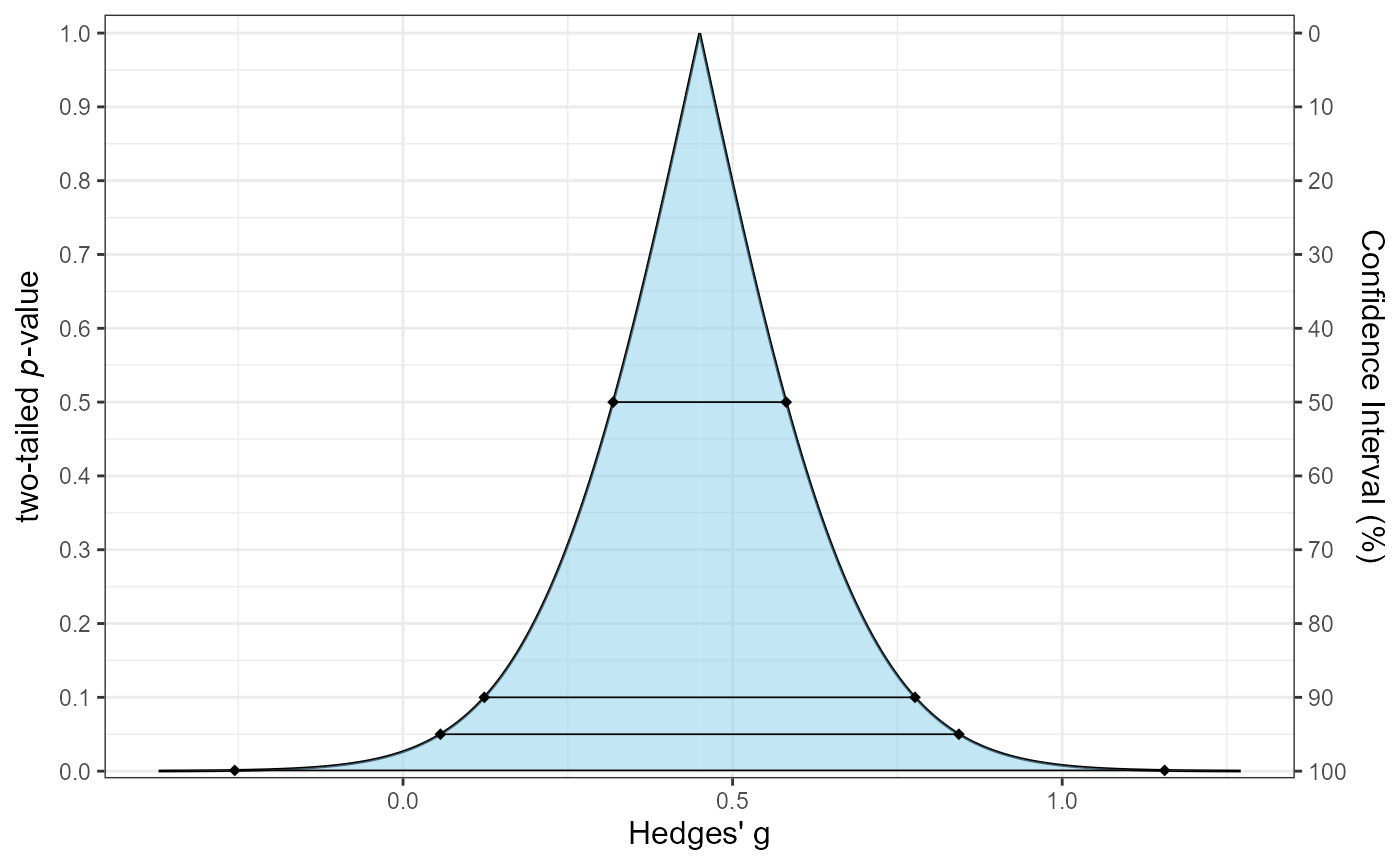 # Example 3: Consonance density only using Goulet method
# Note: lambda parameter required for Goulet method
plot_smd(d = 0.6, df = 35, lambda = 3.6, smd_ci = "goulet",
type = "cd")
# Example 3: Consonance density only using Goulet method
# Note: lambda parameter required for Goulet method
plot_smd(d = 0.6, df = 35, lambda = 3.6, smd_ci = "goulet",
type = "cd")
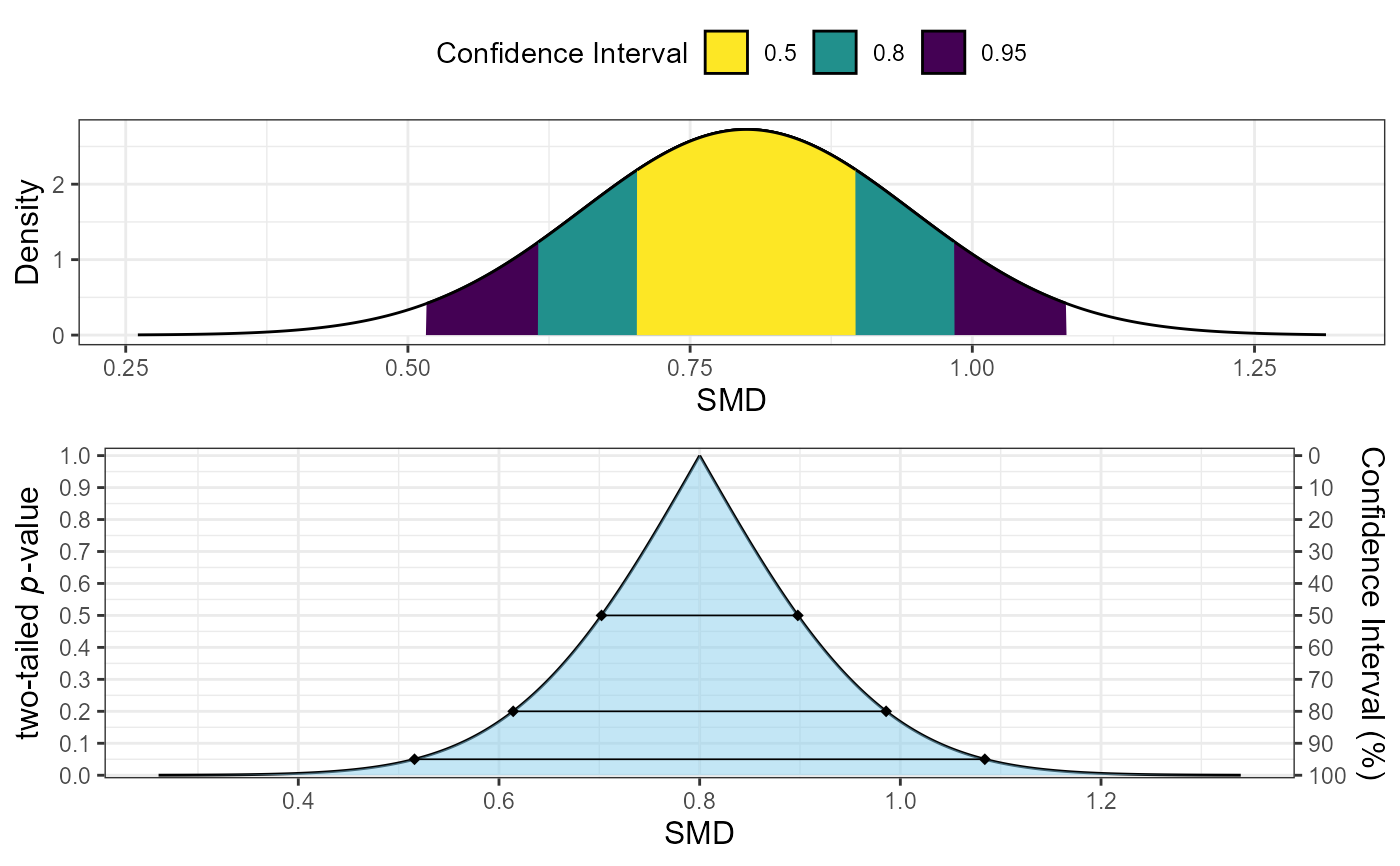
 # Example 4: Custom confidence levels
plot_smd(d = 0.8, df = 50, sigma = 0.145, smd_ci = "z",
levels = c(0.5, 0.8, 0.95))
# Example 4: Custom confidence levels
plot_smd(d = 0.8, df = 50, sigma = 0.145, smd_ci = "z",
levels = c(0.5, 0.8, 0.95))
 # Example 5: Using with TOSTER results (requires extracting needed parameters)
# tost_result <- t_TOST(x = group1, y = group2, eqb = 0.5)
# plot_smd(d = tost_result$smd$d,
# df = tost_result$smd$d_df,
# sigma = tost_result$smd$d_sigma,
# smd_ci = "z",
# smd_label = tost_result$smd$smd_label)
# Example 6: Saving and further customizing the plot
if (FALSE) { # \dontrun{
library(ggplot2)
p <- plot_smd(d = 0.5, df = 40, sigma = 0.164, smd_ci = "z")
p + theme_minimal() +
labs(title = "Consonance Plot for Cohen's d = 0.5",
subtitle = "df = 40")
} # }
# Example 5: Using with TOSTER results (requires extracting needed parameters)
# tost_result <- t_TOST(x = group1, y = group2, eqb = 0.5)
# plot_smd(d = tost_result$smd$d,
# df = tost_result$smd$d_df,
# sigma = tost_result$smd$d_sigma,
# smd_ci = "z",
# smd_label = tost_result$smd$smd_label)
# Example 6: Saving and further customizing the plot
if (FALSE) { # \dontrun{
library(ggplot2)
p <- plot_smd(d = 0.5, df = 40, sigma = 0.164, smd_ci = "z")
p + theme_minimal() +
labs(title = "Consonance Plot for Cohen's d = 0.5",
subtitle = "df = 40")
} # }