Power Analysis and Sample Size Determination for Agreement Studies

Introduction

This vignette provides comprehensive guidance on power analysis and sample size determination for method comparison and agreement studies using the SimplyAgree package.

Available Methods

SimplyAgree implements four approaches to power/sample size calculations:

power_agreement_exact() - Exact agreement test (Shieh 2019)
blandPowerCurve() - Bland-Altman power curves (Lu et al. 2016)
agree_expected_half() - Expected half-width criterion (Jan and Shieh 2018)
agree_assurance() - Assurance probability criterion (Jan and Shieh 2018)

library(SimplyAgree)

Understanding the Approaches

Hypothesis Testing vs. Estimation

The methods divide into two categories:

Hypothesis Testing (binary decision):

power_agreement_exact() - Tests if central proportion, essentially tolerance intevals, are within the maximal allowable difference
blandPowerCurve() - Tests if confidence intervals of limits of agreement fall within the maximal allowable difference

Estimation (quantifying precision):

agree_expected_half() - Controls average CI half-width of limits of agreement
agree_assurance() - Controls probability of achieving target CI half-width of limits of agreement

Method 1: Exact Agreement Test

Overview

Tests whether the central P* proportion of paired differences falls within the maximal allowable difference [-δ, δ].

Hypotheses:

H₀: Methods disagree (central portion extends beyond bounds)
H₁: Methods agree (central portion within bounds)

Usage

power_agreement_exact(
  n = NULL,           # Sample size
  delta = NULL,       # Tolerance bound
  mu = 0,            # Mean of differences
  sigma = NULL,       # SD of differences
  p0_star = 0.95,    # Central proportion (tolerance coverage)
  power = NULL,       # Target power
  alpha = 0.05       # Significance level
)

Specify exactly three of: n, delta, power, sigma.

Example: Sample Size Calculation

# Blood pressure device comparison
result <- power_agreement_exact(
  delta = 7,          # ±7 mmHg tolerance
  mu = 0.5,          # Expected bias
  sigma = 2.5,       # Expected SD
  p0_star = 0.95,    # 95% must be within bounds
  power = 0.80,      # 80% power
  alpha = 0.05
)
#> Maximum iterations reached in gamma computation
print(result)
#> 
#>      Power for Exact Method for Assessing Agreement Between Two Methods 
#> 
#>               n = 34
#>           delta = 7
#>              mu = 0.5
#>           sigma = 2.5
#>         p0_star = 0.95
#>         p1_star = 0.9939889
#>           alpha = 0.05
#>           power = 0.8018321
#>  critical_value = 13.57044
#> 
#> NOTE: H0: Central 95% of differences not within [-delta, delta]
#>      H1: Central 99.4% of differences within [-delta, delta] 
#> n is number pairs. Two measurements per unit; one for each method.

Method 2: Bland-Altman Power Curves

Overview

Calculates power curves using approximate Bland-Altman confidence intervals using the method of Lu et al. (2016) (which is approximate). Useful for exploring power across sample sizes.

Usage

blandPowerCurve(
  samplesizes = seq(10, 100, 1),  # Range of sample sizes
  mu = 0,                          # Mean difference
  SD,                              # SD of differences
  delta,                           # Tolerance bound(s)
  conf.level = 0.95,              # CI confidence level
  agree.level = 0.95               # LOA agreement level
)

Example: Power Curve

# Generate power curve
pc <- blandPowerCurve(
  samplesizes = seq(10, 200, 1),
  mu = 0,
  SD = 3.3,
  delta = 8,
  conf.level = 0.95,
  agree.level = 0.95
)

# Plot
plot(pc, type = 1)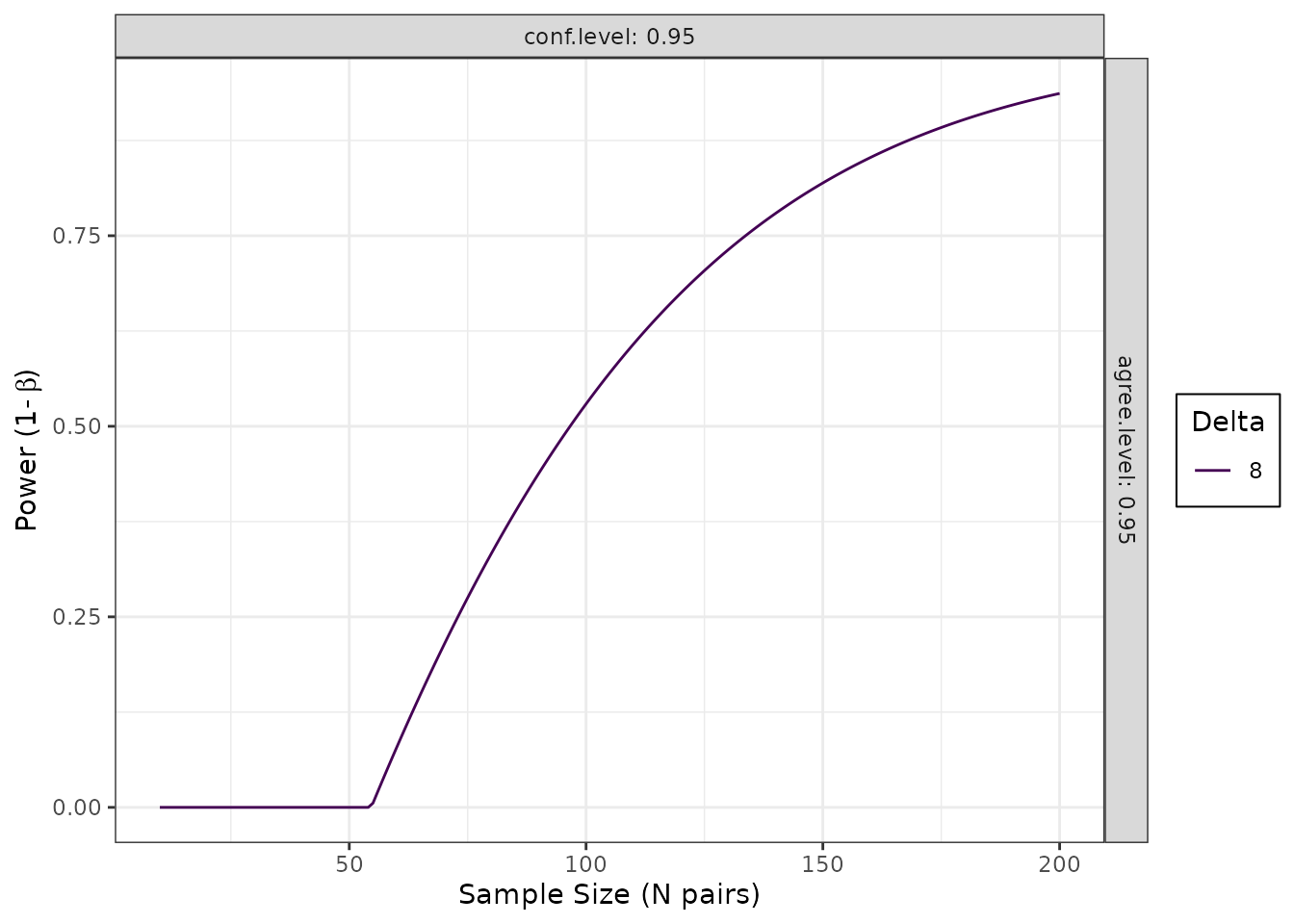


# Find n for 80% power
find_n(pc, power = 0.8)
#> # A tibble: 1 × 5
#>   delta conf.level agree.level power     N
#>   <dbl>      <dbl>       <dbl> <dbl> <dbl>
#> 1     8       0.95        0.95 0.800   145

Method 3: Expected Half-Width

Overview

Determines sample size to ensure average CI half-width ≤ δ across hypothetical repeated studies.

Usage

agree_expected_half(
  conf.level = 0.95,    # CI confidence level
  delta = NULL,         # Target expected half-width
  pstar = 0.95,        # Central proportion
  sigma = 1,           # SD of differences
  n = NULL             # Sample size
)

Specify either n OR delta.

Example: Sample Size for Precision

# Want E[H] ≤ 2.5σ
result <- agree_expected_half(
  conf.level = 0.95,
  delta = 2.5,         # As multiple of sigma
  pstar = 0.95,
  sigma = 1            # Standardized
)
print(result)
#> 
#>      Expected half-width and sample size for limits of agreement 
#> 
#>               n = 52
#>      conf.level = 0.95
#>    target.delta = 2.5
#>    actual.delta = 2.49677
#>           pstar = 0.95
#>           sigma = 1
#>               g = 2.509039
#>               c = 1.004914
#>              zp = 1.959964

Method 4: Assurance Probability

Overview

Determines sample size to ensure probability that CI half-width ≤ ω is at least (1-γ).

Stronger guarantee than expected half-width — ensures specific probability of achieving target precision.

Usage

agree_assurance(
  conf.level = 0.95,     # CI confidence level
  assurance = 0.90,      # Target assurance probability
  omega = NULL,          # Target half-width bound
  pstar = 0.95,         # Central proportion
  sigma = 1,            # SD of differences
  n = NULL              # Sample size
)

Specify either n OR omega.

Example: Sample Size with Guarantee

# Want 90% probability that H ≤ 2.5σ
result <- agree_assurance(
  conf.level = 0.95,
  assurance = 0.90,    # 90% probability
  omega = 2.5,         # Target bound
  pstar = 0.95,
  sigma = 1
)
print(result)
#> 
#>      Assurance probability & sample size for Limits of Agreement 
#> 
#>                n = 115
#>       conf.level = 0.95
#>        assurance = 0.9
#> actual.assurance = 0.9024848
#>            omega = 2.5
#>            pstar = 0.95
#>            sigma = 1
#>                g = 2.306167
#>               zp = 1.959964

Decision Guide for the Method

Research Goal?
│
├─ Hypothesis Testing → 
│   └─ Need exact Type I error control → Power for Agreement
│
└─ Precision Estimation →
    ├─ Average precision sufficient → Expected Half-Width
    └─ Need probabilistic guarantee → Assurance Probability

Handling Clustered/Nested Data

The Problem

Many studies have clustered data where there are multiple measurements per subject or natural groupings (e.g., repeated measures, multi-center studies). Note, the advice here only applies to clustering but not to situations where replicate measures are taken within a measurement occasion (e.g., multiple measures at the same time point wherein any variation would only represent measurement error).

Standard formulas assume independence¹. Ignoring clustering can leads to studies that lack precision. To my knowledge, there is no well developed methods for accounting for clustering in sample size calculations for agreement studies, so we use a common approximation from survey sampling and multilevel modeling: the design effect.

My Best Approximation: Design Effect

The design effect (DEFF) quantifies loss of efficiency due to clustering:

\[\text{DEFF} = 1 + (m - 1) \times \text{ICC}\]

where:

m = observations per cluster
ICC = intraclass correlation coefficient
\(n_{ESS}\) = effective sample size

Effect on sample size: \[n_{\text{ESS}} = n_{\text{independent}} \times \text{DEFF}\]

Understanding ICC

ICC = proportion of variance between clusters:

\[\text{ICC} = \frac{\sigma^2_{\text{between}}}{\sigma^2_{\text{between}} + \sigma^2_{\text{within}}}\]

Application Workflow

Calculate independent sample size (using power function)
Determine m (observations per cluster)
Estimate ICC (from pilot data, literature, or theory)
Calculate DEFF = 1 + (m-1)×ICC
Inflate: n_total = n_indep × DEFF
Calculate clusters: K = ⌈n_total / m⌉

Example: Repeated Measures Design

# Step 1: Independent sample size
result <- power_agreement_exact(
  delta = 7, mu = 0.5, sigma = 2.5,
  p0_star = 0.95, power = 0.80, alpha = 0.05
)
#> Maximum iterations reached in gamma computation
n_indep <- result$n
cat("Independent pairs needed:", n_indep, "\n")
#> Independent pairs needed: 34

# Step 2: Apply design effect
m <- 3  # 3 measurements per participant
ICC <- 0.15  # from pilot or literature
DEFF <- 1 + (m - 1) * ICC
cat("Design effect:", round(DEFF, 3), "\n")
#> Design effect: 1.3

# Step 3: Calculate participants needed
n_ess <- ceiling(n_indep * DEFF)
K <- ceiling(n_ess / m)
cat("Total observations:", n_ess, "\n")
#> Total observations: 45
cat("Participants needed:", K, "\n")
#> Participants needed: 15

Result: Instead of 34 independent pairs, need ~15 participants (45 total observations).

Impact of ICC

# Compare different ICC values
n_indep <- 50
m <- 4

ICC_values <- c(0, 0.05, 0.10, 0.15, 0.20)
for (ICC in ICC_values) {
  DEFF <- 1 + (m - 1) * ICC
  K <- ceiling(ceiling(n_indep * DEFF) / m)
  cat(sprintf("ICC = %.2f: Need %d participants\n", ICC, K))
}
#> ICC = 0.00: Need 13 participants
#> ICC = 0.05: Need 15 participants
#> ICC = 0.10: Need 17 participants
#> ICC = 0.15: Need 19 participants
#> ICC = 0.20: Need 20 participants

When Design Effect Works Well

✓ Good situations:

Balanced designs (equal cluster sizes)
Moderate ICC (0.01 - 0.30)
Sufficient clusters (K ≥ 10)
Simple two-level hierarchy

✗ Problematic:

Highly unbalanced clusters
Very high ICC (> 0.4)
Small number of clusters (K < 10)
Complex correlation structures
Multiple levels of nesting

For complex designs, consider simulation-based power analysis and consult a statistician.

Complete Example with Clustering

# Study parameters
sigma <- 3.3
delta <- 7
m <- 4  # measurements per participant
ICC <- 0.15
dropout <- 0.20

# Step 1: Independent sample size
result <- power_agreement_exact(
  delta = delta, mu = 0, sigma = sigma,
  p0_star = 0.95, power = 0.80, alpha = 0.05
)
#> Maximum iterations reached in gamma computation

# Step 2: Account for clustering
DEFF <- 1 + (m - 1) * ICC
n_total <- ceiling(result$n * DEFF)
K_pre <- ceiling(n_total / m)

# Step 3: Account for dropout
K_final <- ceiling(K_pre / (1 - dropout))

# Summary
cat("Independent pairs:", result$n, "\n")
#> Independent pairs: 566
cat("Design effect:", round(DEFF, 3), "\n")
#> Design effect: 1.45
cat("Participants (no dropout):", K_pre, "\n")
#> Participants (no dropout): 206
cat("Participants to recruit:", K_final, "\n")
#> Participants to recruit: 258
cat("Total measurements:", K_final * m, "\n")
#> Total measurements: 1032

Practical Recommendations

Planning Checklist

Define research question (hypothesis test vs. estimation)
Choose appropriate power method
If possible, obtain pilot estimates (σ, ICC if clustered)
Calculate independent sample size
Adjust for clustering (if applicable)
Adjust for dropout
Conduct sensitivity analyses
Document all assumptions and sources
Pre-register before data collection

Conservative Planning

When uncertain:

Use upper range of plausible σ estimates
Use upper range of plausible ICC estimates
Build in 10-20% buffer beyond calculated required sample size
Conduct sensitivity analyses for key parameters (σ, ICC, etc)

References

Bland, J. Martin. 2003. “Cluster Randomised Trials in the Medical Literature: Two Bibliometric Surveys.” Talk presented to the RSS Medical Section and RSS Liverpool Local Group. https://www-users.york.ac.uk/~mb55/talks/clusml.htm.

Jan, Show-Li, and Gwowen Shieh. 2018. “The Bland-Altman Range of Agreement: Exact Interval Procedure and Sample Size Determination.” Comput. Biol. Med. 100 (September): 247–52.

Lu, Meng-Jie, Wei-Hua Zhong, Yu-Xiu Liu, Hua-Zhang Miao, Yong-Chang Li, and Mu-Huo Ji. 2016. “Sample Size for Assessing Agreement Between Two Methods of Measurement by Bland-Altman Method.” The International Journal of Biostatistics 12 (2). https://doi.org/10.1515/ijb-2015-0039.

Shieh, Gwowen. 2019. “Assessing Agreement Between Two Methods of Quantitative Measurements: Exact Test Procedure and Sample Size Calculation.” Statistics in Biopharmaceutical Research 12 (3): 352–59. https://doi.org/10.1080/19466315.2019.1677495.

Aaron R. Caldwell

Last Updated: 2025-11-19

Introduction

Available Methods

Understanding the Approaches

Hypothesis Testing vs. Estimation

Method 1: Exact Agreement Test

Overview

Usage

Example: Sample Size Calculation

Method 2: Bland-Altman Power Curves

Overview

Usage

Example: Power Curve

Method 3: Expected Half-Width

Overview

Usage

Example: Sample Size for Precision

Method 4: Assurance Probability

Overview

Usage

Example: Sample Size with Guarantee

Decision Guide for the Method

Handling Clustered/Nested Data

The Problem

My Best Approximation: Design Effect

Understanding ICC

Application Workflow

Example: Repeated Measures Design

Impact of ICC

When Design Effect Works Well

Complete Example with Clustering

Practical Recommendations

Planning Checklist

Conservative Planning

References