Agreement Tests

Aaron R. Caldwell

Last Updated: 2024-10-24

Source: vignettes/agree_tests.Rmd

The SimplyAgree R package was created to make the process of quantifying measurement agreement, consistency, and reliability. This package expands upon the capabilities of currently available R packages (such as psych and blandr) by 1) providing support for agreement studies that involve multiple observations (agree_test and agree_reps functions) 2) provide robust tests of agreement even in simple studies (shieh_test output from the agree_test function) and 3) a robust set of reliability statistics (reli_stats function).

In this vignette I will briefly demonstrate the implementation of the functions that include tests of agreement. Please note, I would recommend using the agreement_limit function over these older functions with the exception of agree_np which provides non-parametric agreement limits.

Simple Agreement

agree_test

In the simplest scenario, a study may be conducted to compare one measure (e.g., x) and another (e.g., y). In this scenario each pair of observations (x and y) are independent; meaning that each pair represents one subject/participant. In most cases we have a degree of agreement that we would deem adequate. This may constitute a hypothesis wherein you may believe the agreement between two measurements is within a certain limit (limits of agreement). If this is the goal then the agree_test function is what you need to use in this package.

The data for the two measurements are put into the x and y arguments. If there is a hypothesized limit of agreement then this can be set with the delta argument (this is optional). Next, the limit of agreement can be set with the agree.level and the confidence level (1−α1-\alpha). Once those are set the analysis can be run. Please note, this package has pre-loaded data from the Zou 2013 paper. While data does not conform the assumptions of the test it can be used to test out many of the functions in this package. Since there isn’t an a priori hypothesis I will not declare a delta argument, but I will estimate the 95% confidence intervals for 80% limits of agreement.

a1 = agree_test(x = reps$x,
                y = reps$y,
                agree.level = .8)
#> Warning: `agree_test()` was deprecated in SimplyAgree 0.2.0.
#> ℹ Please use `agreement_limit()` instead.
#> This warning is displayed once every 8 hours.
#> Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
#> generated.

We can then print the general results. These results include the general parameters of the analysis up top, then the results of the Shieh exact test for agreement (no conclusion is included due to the lack of a delta argument being set). Then the limits of agreement, with confidence limits, are included. Lastly, Lin’s Concordance Correlation Coefficient, another measure of agreement, is also included.

print(a1)
#> Limit of Agreement = 80%
#> 
#> ###- Shieh Results -###
#> Exact 90% C.I.  [-1.512, 2.3887]
#> Hypothesis Test: No Hypothesis Test
#> 
#> ###- Bland-Altman Limits of Agreement (LoA) -###
#>           Estimate Lower CI Upper CI CI Level
#> Bias        0.4383  -0.1669   1.0436     0.95
#> Lower LoA  -1.1214  -1.8037  -0.4391     0.90
#> Upper LoA   1.9980   1.3157   2.6803     0.90
#> 
#> ###- Concordance Correlation Coefficient (CCC) -###
#> CCC: 0.4791, 95% C.I. [0.1276, 0.7237]

Next, we can use the generic plot function to produce visualizations of agreement. This includes the Bland-Altman plot (type = 1) and a line-of-identity plot (type = 2).

plot(a1, type = 1)


plot(a1, type = 2)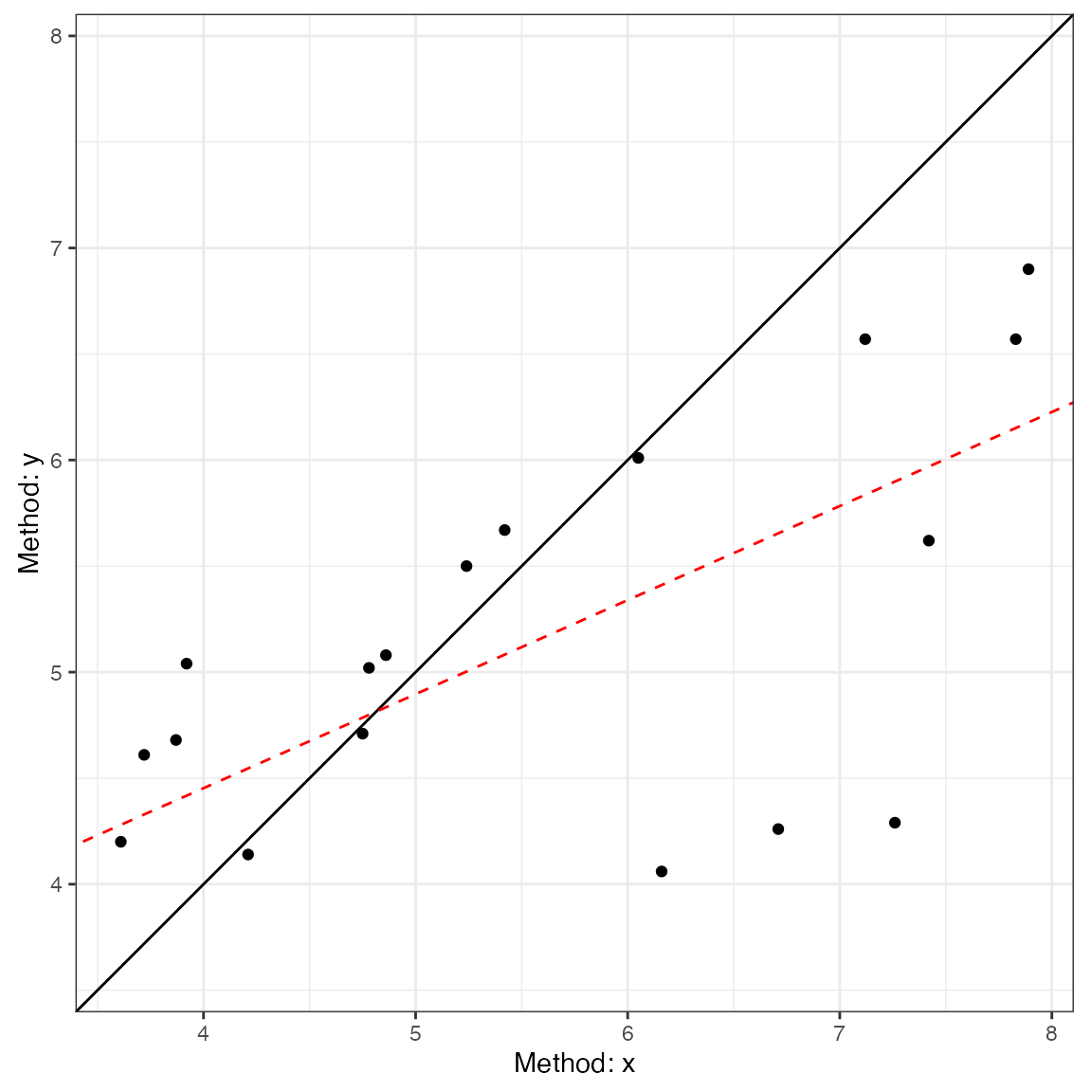

Calculations in for Simple Agreement

Shieh’s test

The hypothesis test procedure is based on the “exact” approach details by Shieh (2019). In this procedure the null hypothesis (not acceptable agreement) is rejected if the extreme lower bound and upper bound are within the proposed agreement limits. The agreement limits ($\hat\theta_{EL} \space and \space \hat\theta_{EU}$) are calculated as the following:

θ̂EL,EU=d‾±γ1−α⋅SN \hat\theta_{EL,EU} = \bar{d} \pm \gamma_{1-\alpha}\cdot \frac{S}{\sqrt{N}}

wherein d‾\bar{d} is the mean difference between the two methods, SS is the standard deviation of the differences, NN is the total number of pairs, and γ1−α\gamma_{1-\alpha} critical value (which requires a specialized function within R to estimate).

Limits of Agreement

The reported limits of agreement are derived from the work of Bland and Altman (1986) and Bland and Altman (1999).

LoA

LoA=d‾±z1−(1−agree)/2⋅Sd LoA = \bar d \pm z_{1-(1-agree)/2} \cdot S_d wherein z1−(1−agree)/2z_{1-(1-agree)/2} is the value of the normal distribution at the given agreement level (default is 95%), d‾\bar d is the mean of the differences, and SdS_d is the standard deviations of the differences.

Confidence Interval

LoAC.I.=LoA±t1−α/2,N−1⋅[1N+(z1−α/2)22⋅(N−1)]⋅S2 LoA_{C.I.} = LoA \pm t_{1-\alpha/2,N-1} \cdot \sqrt{\left[\frac{1}{N}+\frac{(z_{1-\alpha/2})^{2}}{2 \cdot (N-1)} \right] \cdot S^2}

wherein, tt is the critical t-value at the given sample size and confidence level (conf.level), zz is the value of the normal distribution at the given alpha level (agree.level), and S2S^2 is the variance of the difference scores. If TOST is set to TRUE then equation is altered slightly with the critical t (t1−α,N−1t_{1-\alpha,N-1}).

Concordance Correlation Coefficient

The CCC was calculated as outlined by Lin (1989) (with later corrections).

ρ̂c=2⋅sxysx2+sy2+(x‾−y‾)2 \hat\rho_c = \frac{2 \cdot s_{xy}} {s_x^2 + s_y^2+(\bar x-\bar y)^2} where sxys_{xy} is the covariance, sx2s_x^2 and sy2s_y^2 are the variances of x and y respectively, and (x‾−y‾)(\bar x-\bar y) is the difference in the means of x & y.

Repeated Measures Agreement

In many cases there are multiple measurements taken within subjects when comparing two measurements tools. In some cases the true underlying value will not be expected to vary (i.e., replicates; agree_reps), or multiple measurements may be taken within an individual and these values are expected to vary (i.e., nested design; agree_nest).

The confidence limits on the limits of agreement are based on the “MOVER” method described in detail by Zou (2011). However, both functions operate similarly to agree_test; the only difference being that the data has to be provided as a data.frame in R.

agree_reps

This function is for cases where the underlying values do not vary within subjects. This can be considered cases where replicate measure may be taken. For example, a researcher may want to compare the performance of two ELISA assays where measurements are taken in duplicate/triplicate.

So, for this function you will have to provide the data frame object with the data argument and the names of the columns containing the first (x argument) and second (y argument) must then be provided. An additional column indicating the subject identifier (id) must also be provided. Again, if there is a hypothesized agreement limit then this could be provided with the delta argument.

a2 = agree_reps(x = "x",
                y = "y",
                id = "id",
                data = reps,
                agree.level = .8)
#> Warning: `agree_reps()` was deprecated in SimplyAgree 0.2.0.
#> ℹ Please use `agreement_limit()` instead.
#> This warning is displayed once every 8 hours.
#> Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
#> generated.

The results can then be printed. The printing format is very similar to agree_test, but notice that 1) the hypothesis test is based on the limits of agreement (MOVER method), 2) the Concordance Correlation Coefficient is calculated via the U-statistics method, 3) the Shieh TOST results are missing because they cannot be estimated for this type of design.

print(a2)
#> Limit of Agreement = 80%
#> Replicate Data Points (true value does not vary)
#> 
#> Hypothesis Test: No Hypothesis Test
#> 
#> ###- Bland-Altman Limits of Agreement (LoA) -###
#>           Estimate Lower CI Upper CI CI Level
#> Bias        0.7152  -0.6667   2.0971     0.95
#> Lower LoA  -1.2117  -4.7970   0.1054     0.90
#> Upper LoA   2.6421   1.3250   6.2274     0.90
plot(a2, type = 1)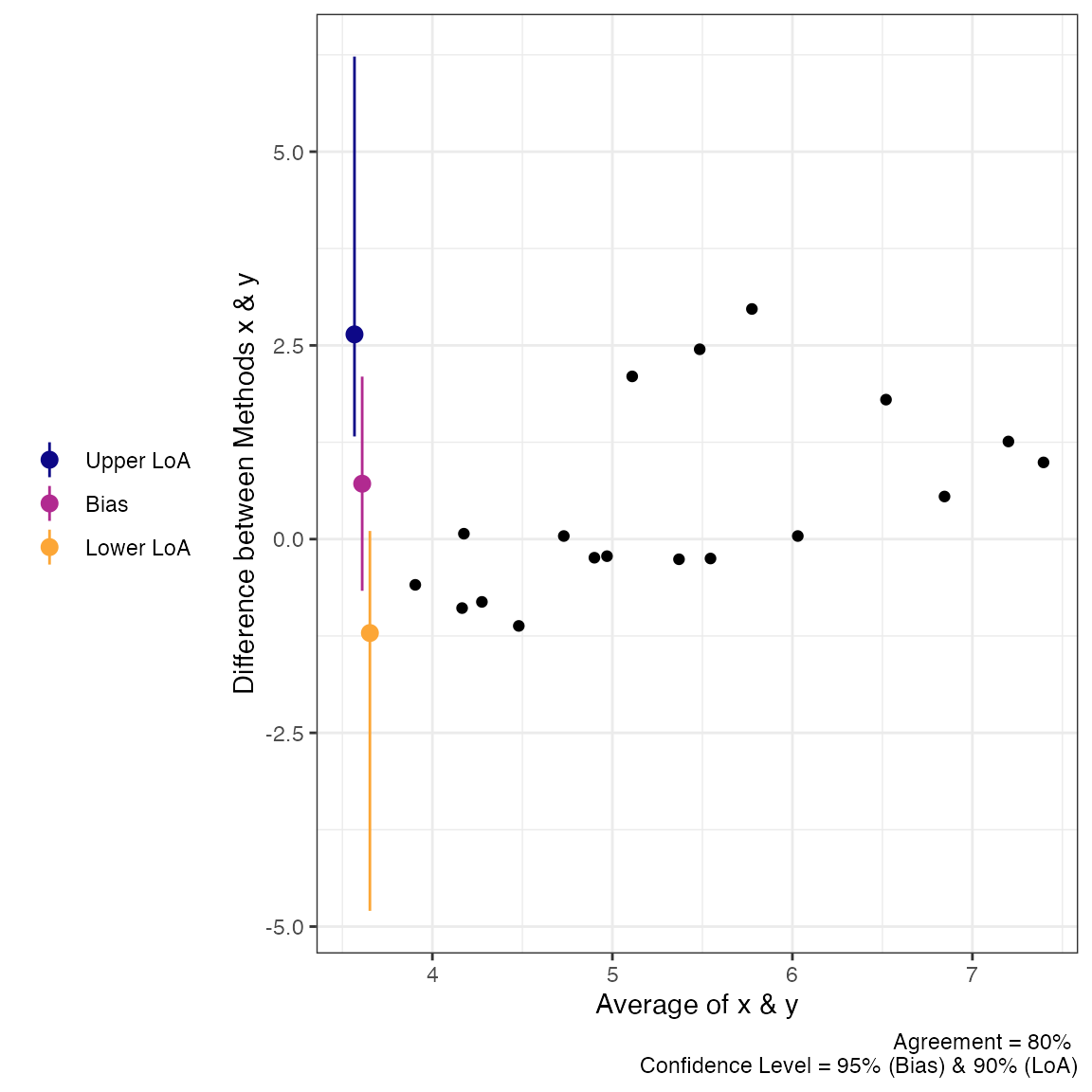


plot(a2, type = 2)

agree_nest

This function is for cases where the underlying values may vary within subjects. This can be considered cases where there are distinct pairs of data wherein data is collected in different times/conditions within each subject. An example would be measuring blood pressure on two different devices on many people at different time points/days.

The function works almost identically to agree_reps but the underlying calculations are different

a3 = agree_nest(x = "x",
                y = "y",
                id = "id",
                data = reps,
                agree.level = .8)
#> Warning: `agree_nest()` was deprecated in SimplyAgree 0.2.0.
#> ℹ Please use `agreement_limit()` instead.
#> This warning is displayed once every 8 hours.
#> Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
#> generated.

The printed results (and plots) are very similar to agree_reps. However, the CCC result now has a warning because the calculation in this scenario may not be entirely appropriate given the nature of the data.

print(a3)
#> Limit of Agreement = 80%
#> Nested Data Points (true value may vary)
#> 
#> Hypothesis Test: No Hypothesis Test
#> 
#> ###- Bland-Altman Limits of Agreement (LoA) -###
#>           Estimate Lower CI Upper CI CI Level
#> Bias        0.7101  -0.6824   2.1026     0.95
#> Lower LoA  -1.1626  -4.8172   0.1811     0.90
#> Upper LoA   2.5828   1.2390   6.2374     0.90
plot(a3, type = 1)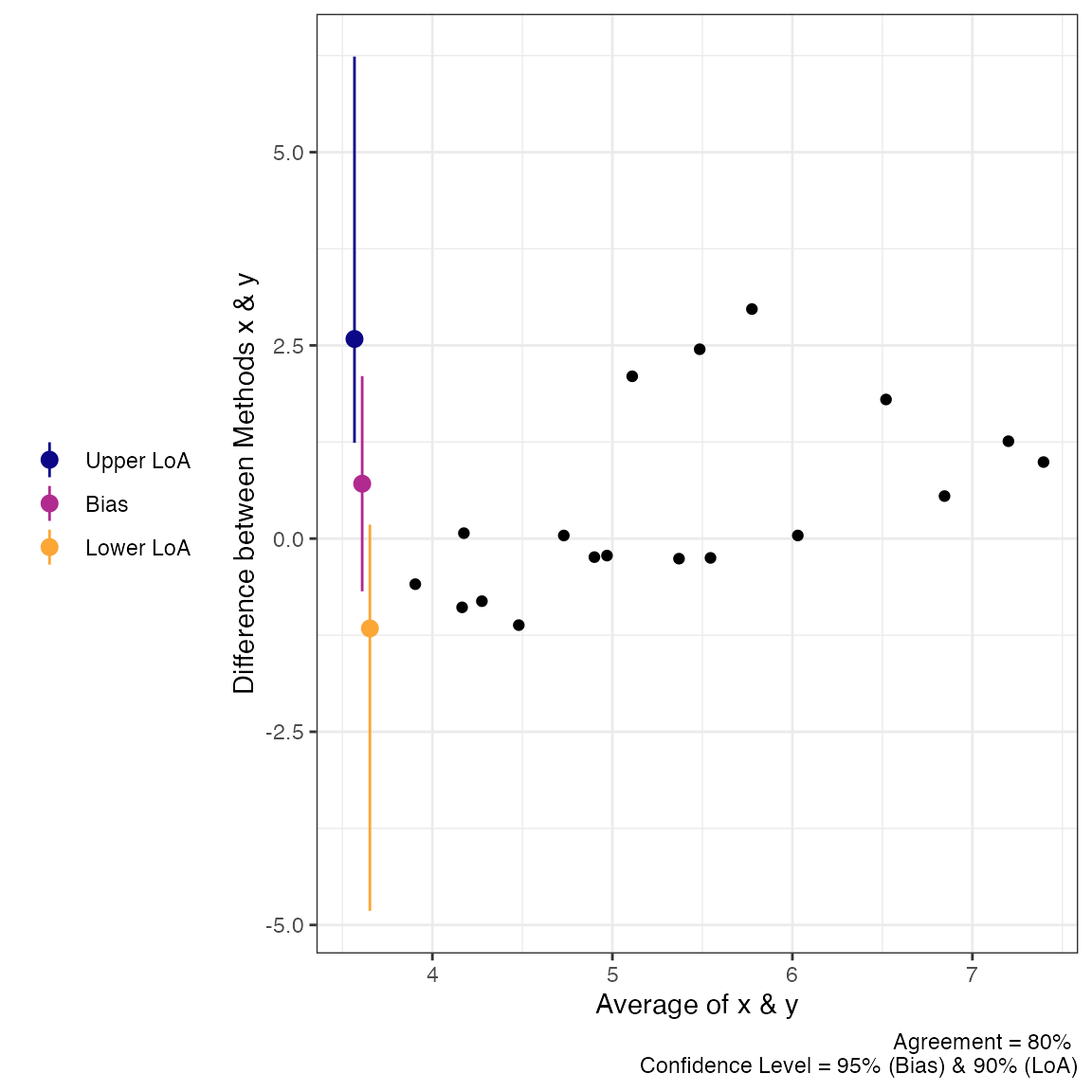


plot(a3, type = 2)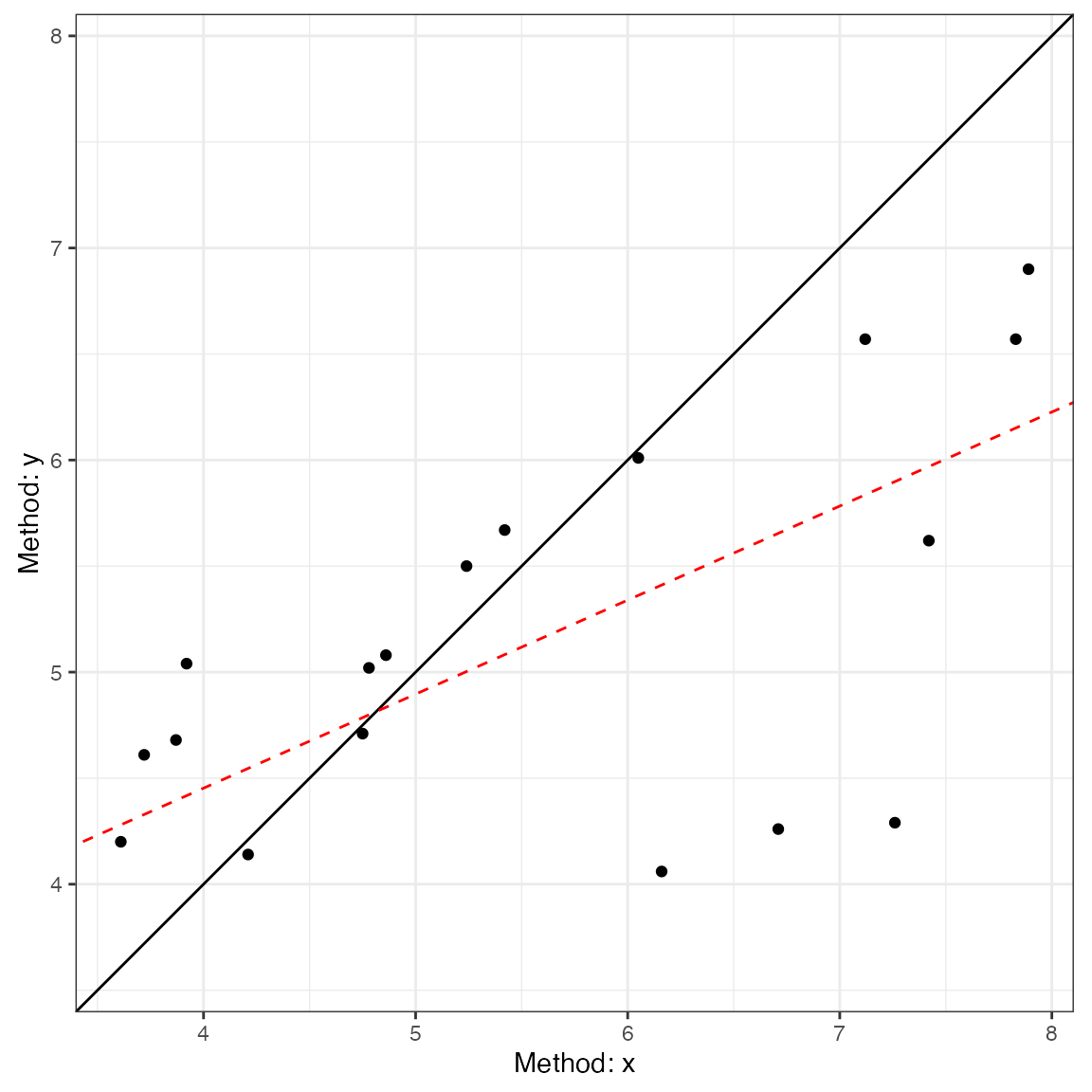

Calculations for agree_reps & agree_nest

All the calculations for the limits of agreement in these two functions can be found in the article by Zou (2011).

agree_nest LoA

Step 1: Calculate Individual Subject Means and Variances

x‾i=1nxiΣj=1nxixij \bar x_i = \frac{1}{n_{xi}} \Sigma_{j=1}^{n_{xi}} x_{ij} y‾i=1nyiΣj=1nyiyij \bar y_i = \frac{1}{n_{yi}} \Sigma_{j=1}^{n_{yi}} y_{ij} d‾i=x‾i−y‾i \bar d_i = \bar x_i - \bar y_i

d‾=Σi=1ndin \bar d = \Sigma_{i=1}^{n}\frac{d_i}{n}

sxi2=Σj=1nxi(xxj−x‾i)2nxi−1 s_{xi}^2 = \Sigma_{j=1}^{n_{xi}} \frac{(x_{xj}- \bar x_i)^2}{n_{xi}-1}

syi2=Σj=1nyi(yij−y‾i)2nyi−1 s_{yi}^2 = \Sigma_{j=1}^{n_{yi}} \frac{(y_{ij}- \bar y_i)^2}{n_{yi}-1}

sd‾2=Σj=1n(di−d‾)2n−1 s_{\bar d}^2 = \Sigma_{j=1}^{n} \frac{(d_{i}- \bar d)^2}{n-1}

Step 2: Compute pooled estimates of within subject errors

sxw2=Σi=1n[nxi−1Nx−1⋅sxi2] s^2_{xw} = \Sigma_{i=1}^{n} [\frac{n_{xi} -1}{N_x -1} \cdot s^2_{xi}]

syw2=Σi=1n[nyi−1Ny−1⋅syi2] s^2_{yw} = \Sigma_{i=1}^{n} [\frac{n_{yi} -1}{N_y -1} \cdot s^2_{yi}]

Step 3: Compute Harmonic Means of Replicates

mxh=nΣi=1n1nxi m_{xh} = \frac{n}{\Sigma_{i=1}^n \frac{1}{n_{xi}}}

myh=nΣi=1n1nyi m_{yh} = \frac{n}{\Sigma_{i=1}^n \frac{1}{n_{yi}}} Step 4: Compute the variance of the differences

sd2=sd‾2+(1+1mxh)⋅sxw2+(1+1myh)⋅syw2 s^2_d = s^2_{\bar d} + (1+\frac{1}{m_{xh}}) \cdot s^2_{xw} + (1+\frac{1}{m_{yh}}) \cdot s^2_{yw} Step 5: Compute MOVER Components

S11=sd‾2⋅(1−n−1χ(1−α,n−1)2) S_{11} = s_{\bar d}^2 \cdot (1 - \frac{n-1}{\chi^2_{(1-\alpha, n-1)}})

S12=(1−1mxh)⋅(1−Nx−nχ(1−α,Nx−n)2)⋅sxw2 S_{12} = (1-\frac{1}{m_{xh}}) \cdot (1 - \frac{N_x-n}{\chi^2_{(1-\alpha, N_x-n)}}) \cdot s^2_{xw} S13=(1−1myh)⋅(1−Ny−nχ(1−α,Ny−n)2)⋅syw2 S_{13} = (1-\frac{1}{m_{yh}}) \cdot (1 - \frac{N_y-n}{\chi^2_{(1-\alpha, N_y-n)}}) \cdot s^2_{yw}

S1=S112+S122+S132 S_1 = \sqrt{S_{11}^2 +S_{12}^2 +S_{13}^2} l=sd2−S1 l = s_d^2 - S_1

u=sd2+S1 u = s_d^2 + S_1

LME=zα2⋅sd2n+zβ/22⋅(u−sd2)2 LME = \sqrt{\frac{z^2_{\alpha} \cdot s_d^2}{n} + z^2_{\beta/2} \cdot(\sqrt{u} - \sqrt{s^2_d})^2}

RME=zα2⋅sd2n+zβ/22⋅(l−sd2)2 RME = \sqrt{\frac{z^2_{\alpha} \cdot s_d^2}{n} + z^2_{\beta/2} \cdot(\sqrt{l} - \sqrt{s^2_d})^2} ### LoA

LoAlower=d‾−zβ/2⋅sd LoA_{lower} = \bar d - z_{\beta/2} \cdot s_d

LoAupper=d‾+zβ/2⋅sd LoA_{upper} = \bar d + z_{\beta/2} \cdot s_d

Lower LoA CI

$$ Lower \space CI = LoA_{lower} - LME $$

$$ Upper \space CI = LoA_{lower} + RME $$

Upper LoA CI

$$ Lower \space CI = LoA_{upper} - RME $$

$$ Upper \space CI = LoA_{upper} + LME $$

agree_reps LoA

LoA

Step 1: Compute mean and variance

d‾i=Σj=1nidijni \bar d_i = \Sigma_{j=1}^{n_i} \frac{d_{ij}}{n_i} d‾=Σi=1ndin \bar d = \Sigma^{n}_{i=1} \frac{d_i}{n}

si2=Σj=1ni(dij−d‾i)2ni−1 s_i^2 = \Sigma_{j=1}^{n_i} \frac{(d_{ij} - \bar d_i)^2}{n_i-1} Step 2: Compute pooled estimate of within subject error

sdw2=Σi=1n[ni−1N−n⋅si2] s_{dw}^2 = \Sigma_{i=1}^{n} [\frac{n_i-1}{N-n} \cdot s_i^2]

Step 3: Compute pooled estimate of between subject error

sb2=Σi=1n(d‾i−d‾)2n−1 s^2_b = \Sigma_{i=1}^n \frac{ (\bar d_i - \bar d)^2}{n-1}

Step 4: Compute the harmonic mean of the replicate size

mh=nΣi=1nmi−1 m_h = \frac{n}{\Sigma_{i=1}^n m_i^{-1}}

Step 5: Compute SD of the difference

sd2=sb2+(1+mh−1)⋅sdw2 s_d^2 = s^2_b + (1+m_h^{-1}) \cdot s_{dw}^2 Step 6: Calculate l and u

l=sd2−[sd2⋅(1−n−1χ(1−α,n−1)2)]2+[(1−mh−1)⋅(1−N−nχ(1−α,N−n)2)]2 l = s_d^2 - \sqrt{[s_d^2 \cdot (1 - \frac{n-1}{\chi^2_{(1-\alpha, n-1)}})]^2+[(1-m_h^{-1}) \cdot (1- \frac{N-n}{\chi^2_{(1-\alpha, N-n)}})]^2} u=sd2+[sd2⋅(1−n−1χ(1−α,n−1)2)]2+[(1−mh−1)⋅(1−N−nχ(1−α,N−n)2)]2 u = s_d^2 + \sqrt{[s_d^2 \cdot (1 - \frac{n-1}{\chi^2_{(1-\alpha, n-1)}})]^2+[(1-m_h^{-1}) \cdot (1- \frac{N-n}{\chi^2_{(1-\alpha, N-n)}})]^2} Step 7: Compute LME and RME

LME=zα⋅sd2n+zβ/22⋅(u−sd2)2 LME = \sqrt{\frac{z_{\alpha} \cdot s_d^2}{n} + z_{\beta/2}^2 \cdot (\sqrt{u}-\sqrt{s^2_d} )^2}

RME=zα⋅sd2n+zβ/22⋅(l−sd2)2 RME = \sqrt{\frac{z_{\alpha} \cdot s_d^2}{n} + z_{\beta/2}^2 \cdot (\sqrt{l}-\sqrt{s^2_d} )^2}

LoA

LoAlower=d‾−zβ/2⋅sd LoA_{lower} = \bar d - z_{\beta/2} \cdot s_d

LoAupper=d‾+zβ/2⋅sd LoA_{upper} = \bar d + z_{\beta/2} \cdot s_d

Lower LoA CI

$$ Lower \space CI = LoA_{lower} - LME $$

$$ Upper \space CI = LoA_{lower} + RME $$

Upper LoA CI

$$ Lower \space CI = LoA_{upper} - RME $$

$$ Upper \space CI = LoA_{upper} + LME $$

CCC from U-statistics

The CCC calculations are derived from the cccUst function of the cccrm R package. The mathematics for this CCC calculation can be found in the work of King, Chinchilli, and Carrasco (2007) and Carrasco, King, and Chinchilli (2009).

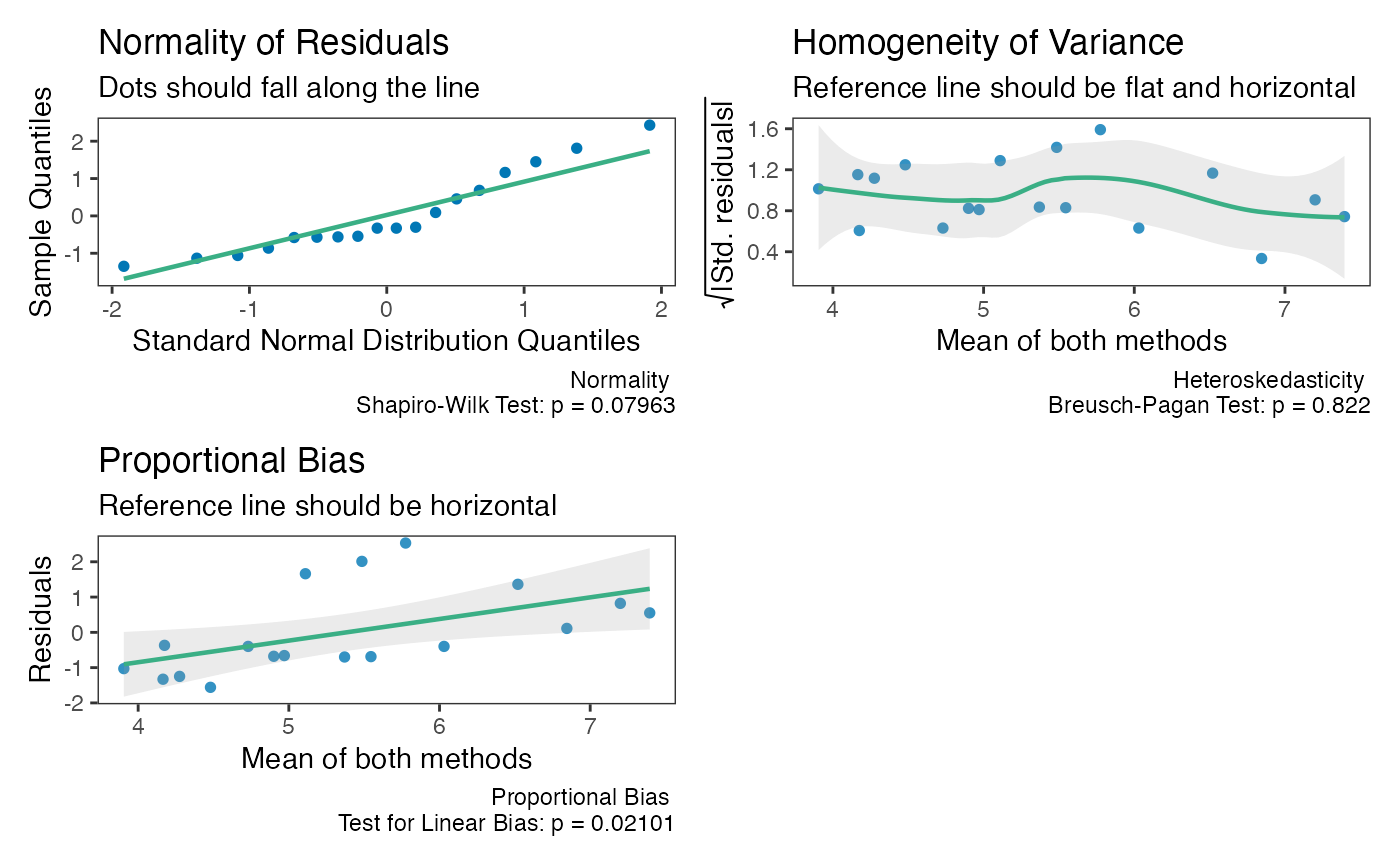
Checking Assumptions

The assumptions of normality, heteroscedasticity, and proportional bias can all be checked using the check method.

The function will provide 3 plots: Q-Q normality plot, standardized residuals plot, and residuals plot.

All 3 plots will have a statistical test in the bottom right corner. The Shapiro-Wilk test is included for the normality plot, the Bagan-Preusch test for heterogeneity, and the test for linear slope on the residuals plot.

An Example 

a1 = agree_test(x = reps$x,
                y = reps$y,
                agree.level = .8)

check(a1)

Proportional Bias

As the check plots for a1 show, proportional bias can sometimes occur. In these cases Bland and Altman (1999) recommended adjusting the bias and LoA for the proportional bias. This is simply done by include a slope for the average of both measurements (i.e, using an intercept + slope model rather than intercept only model).

For any of the “agree” functions, this can be accomplished with the prop_bias argument. When this is set to TRUE, then the proportional bias adjusted model is utilized. However, you should be careful with interpreting the hypothesis tests in these cases because the results are likely bogus for the extreme ends of the measurement. In any case, plots of the data should always be inspected

a1 = agree_test(x = reps$x,
                y = reps$y,
                prop_bias = TRUE,
                agree.level = .8)
#> prop_bias set to TRUE. Hypothesis test may be bogus. Check plots.
print(a1)
#> Limit of Agreement = 80%
#> 
#> ###- Shieh Results -###
#> Exact 90% C.I.  [-1.2551, 2.1318]
#> Hypothesis Test: No Hypothesis Test
#> Warning: hypothesis test likely bogus with proportional bias.
#> ###- Bland-Altman Limits of Agreement (LoA) -###
#>           Estimate Lower CI Upper CI CI Level
#> Bias        0.4383 -0.08968   0.9663     0.95
#> Lower LoA  -0.9159 -1.51049  -0.3213     0.90
#> Upper LoA   1.7926  1.19801   2.3872     0.90
#> 
#> LoA at average of both measures. Please check plot.
#> ###- Concordance Correlation Coefficient (CCC) -###
#> CCC: 0.4791, 95% C.I. [0.1276, 0.7237]

plot(a1)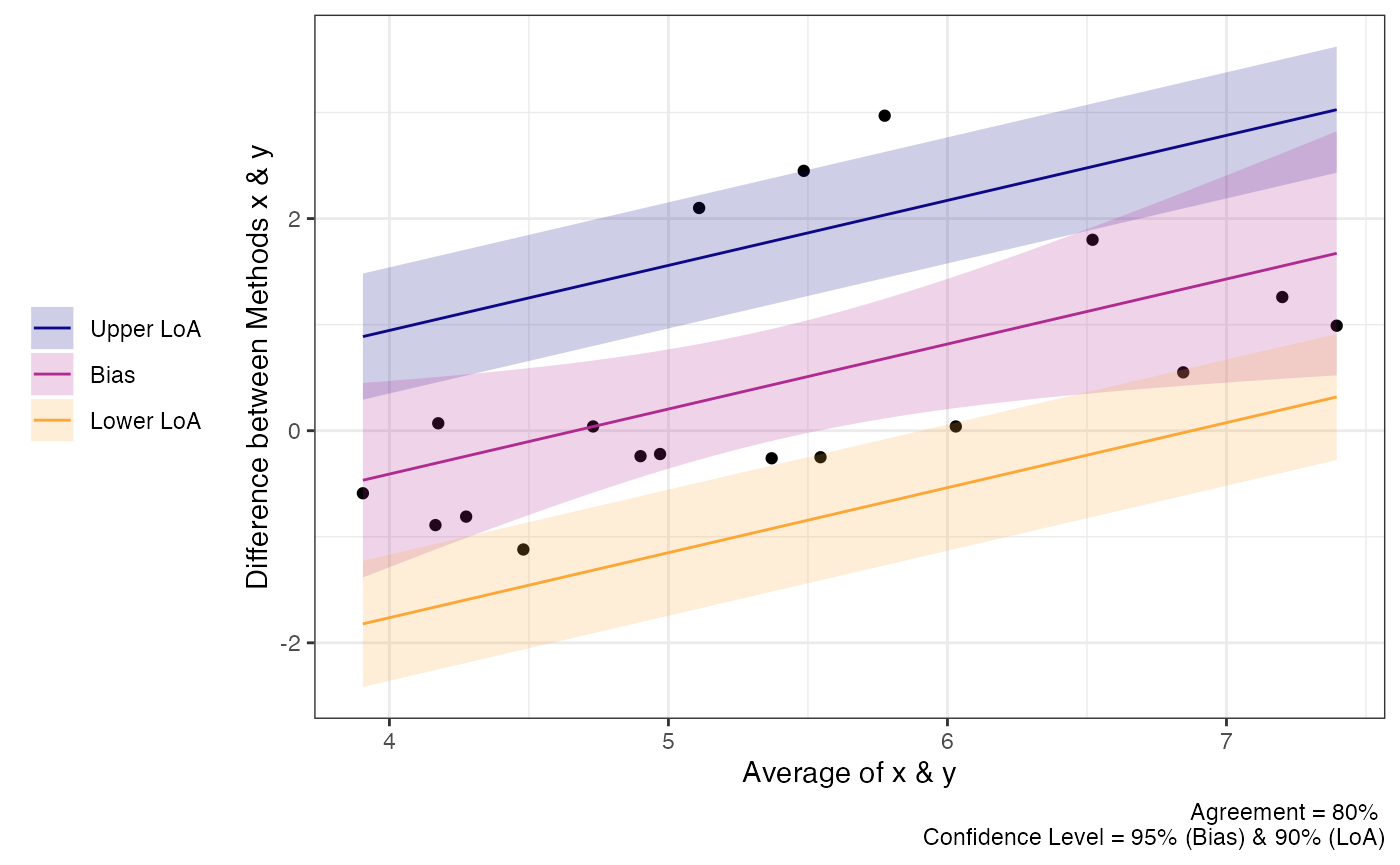

Non-parametric Alternatives

When the assumptions of any of the tests above are violated then a non-parametric alternative may be useful. The agree_np function is the non-parametric alternative for the SimpleAgree R package, and is largely based on the recommendations of Bland & Altman (Bland and Altman 1999, pg. 157).

The function performs two tests:

  1. A binomial test on whether or not the observed differences are within the maximal allowable differences bounds (delta argument).
  2. Quantile regression, derived from the quantreg package (Koenker 2020), two estimate the median and 95% limits of agreement. If the default agreement levels are used (agree.level = .95) then the 0.025, 0.5 (median), and 0.975 quantiles are estimated.

The function also requires the delta argument (otherwise the binomial test would be useless). Otherwise, it functions just like the other agreement functions.

In the code demo below, you will notice that the limits of agreement are no longer symmetric around the bias estimate.

a1 = agree_np(x = "x",
              y = "y",
              data = reps,
              delta = 2,
              prop_bias = FALSE,
              agree.level = .8)
print(a1)
#> Limit of Agreement = 80%
#> Binomial proportions test and quantile regression for LoA
#> 
#>            agreement lower.ci upper.ci
#> % within 2    0.8333   0.5914   0.9453
#> Hypothesis Test: don't reject h0
#> 
#> ###- Quantile Limits of Agreement (LoA) -###
#>           Estimate Lower CI Upper CI CI Level
#> Lower LoA    -0.89  -1.3739  -0.4061     0.90
#> Bias          0.04  -0.5234   0.6034     0.95
#> Upper LoA     2.45   1.4983   3.4017     0.90

plot(a1)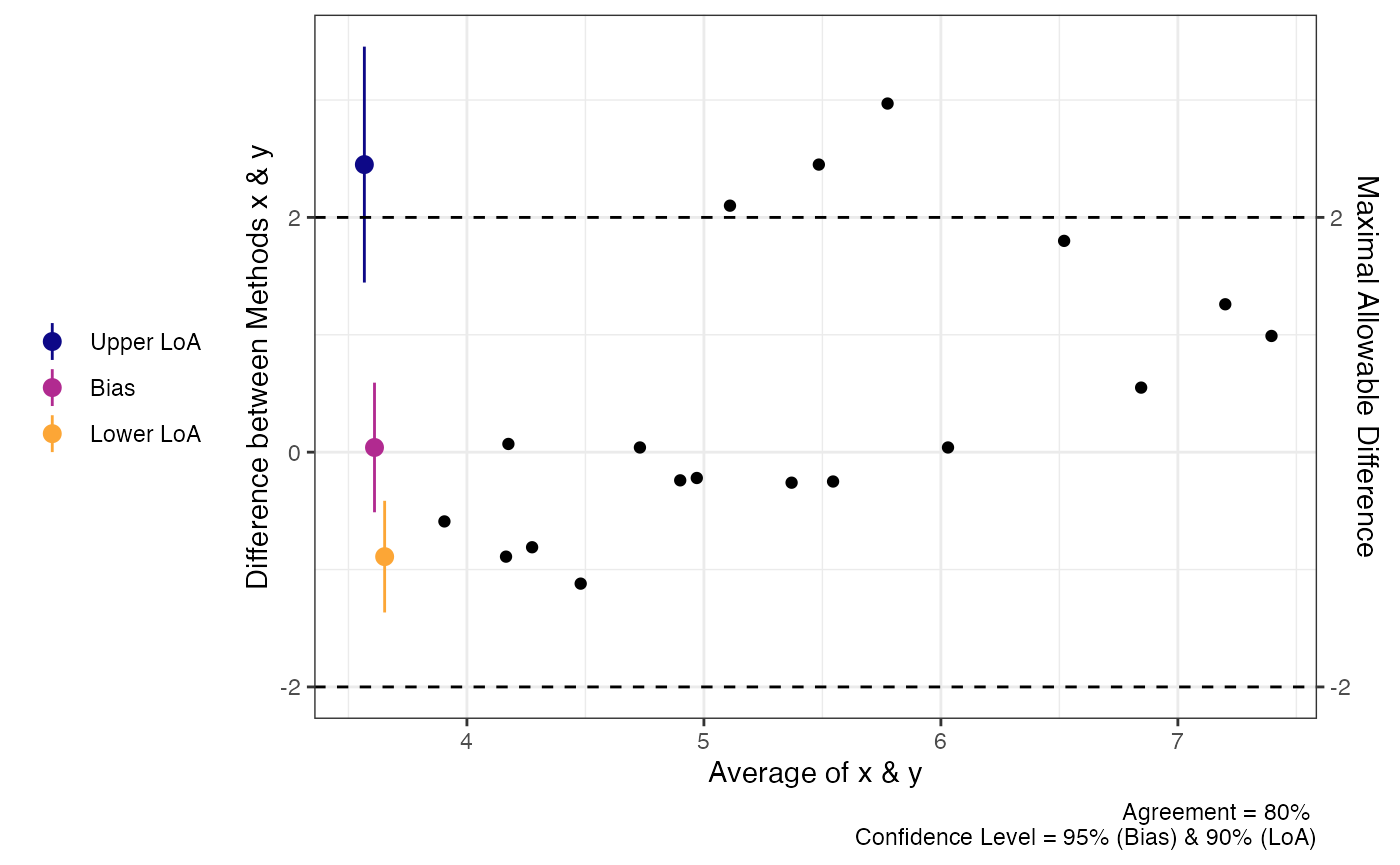

We can also perform the same analysis with proportional bias no longer assumed. You can see that the LoA changes but the test for agreement does not.

a1 = agree_np(x = "x",
              y = "y",
              data = reps,
              delta = 2,
              prop_bias = TRUE,
              agree.level = .8)
print(a1)
#> Limit of Agreement = 80%
#> Binomial proportions test and quantile regression for LoA
#> 
#>            agreement lower.ci upper.ci
#> % within 2    0.8333   0.5914   0.9453
#> Hypothesis Test: don't reject h0
#> 
#> ###- Quantile Limits of Agreement (LoA) -###
#>                  Estimate Lower CI Upper CI CI Level
#> Lower LoA @ 3.9  -1.28975  -1.7203 -0.85925     0.90
#> Lower LoA @ 5.24 -0.45436  -0.6465 -0.26221     0.90
#> Lower LoA @ 7.4   0.89417   0.6088  1.17953     0.90
#> Bias @ 3.9       -0.73052  -1.5079  0.04682     0.95
#> Bias @ 5.24      -0.07238  -0.7088  0.56406     0.95
#> Bias @ 7.4        0.99000  -0.4509  2.43089     0.95
#> Upper LoA @ 3.9  -0.38310  -2.9310  2.16480     0.90
#> Upper LoA @ 5.24  2.01069   1.0814  2.93996     0.90
#> Upper LoA @ 7.4   5.87483   2.3417  9.40794     0.90

plot(a1)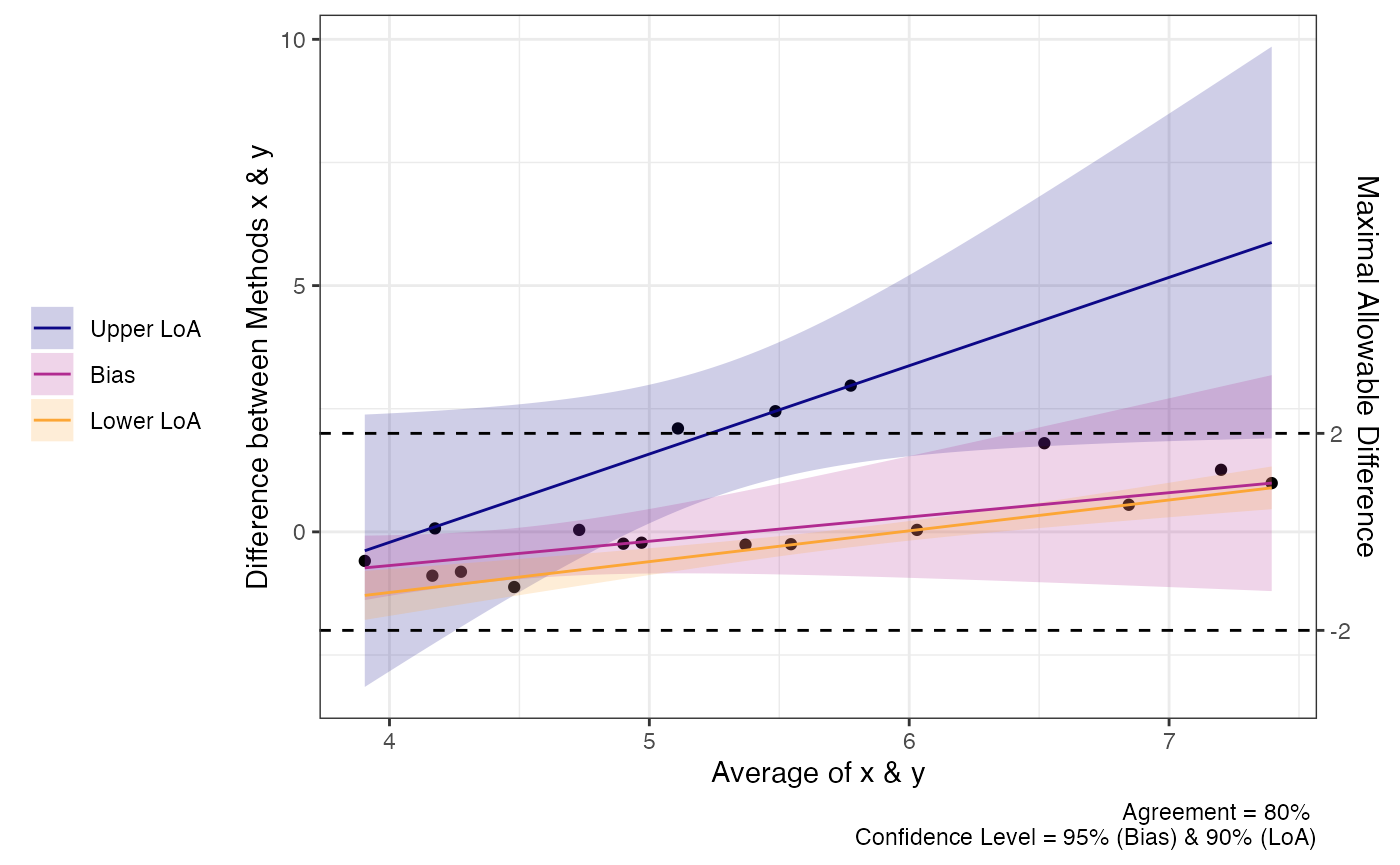

“Big” Data

Sometimes there may be a lot of data and individual points of data on Bland-Altman plot may be less than ideal. In order to change the plots from showing the individual data points we can modify the geom_point argument.

set.seed(81346)
x = rnorm(750, 100, 10)
diff = rnorm(750, 0, 1)
y = x + diff

df = data.frame(x = x,
                y = y)

a1 = agree_test(x = df$x,
                y = df$y,
                agree.level = .95)

plot(a1,
     geom = "geom_point")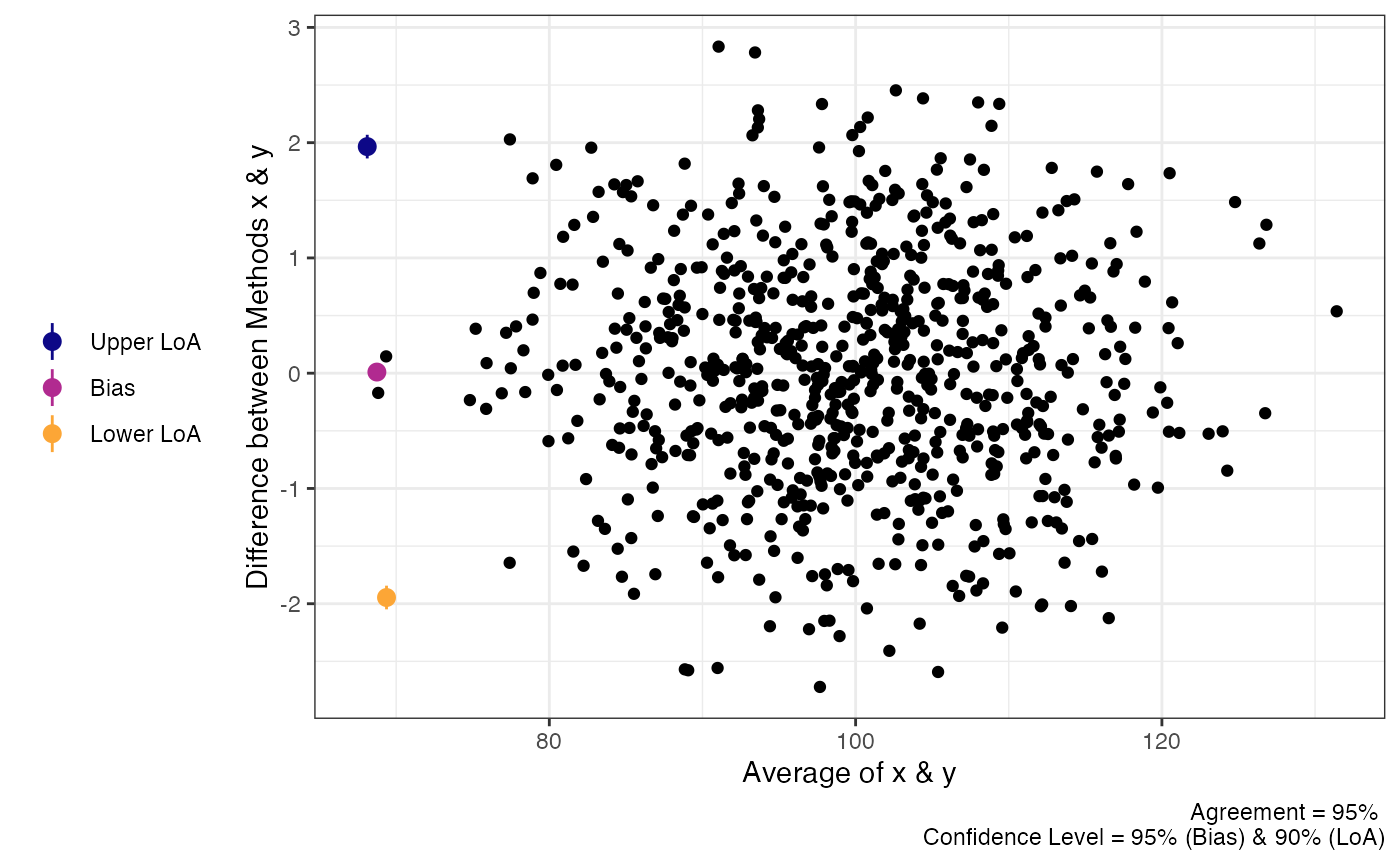


plot(a1,
     geom = "geom_bin2d")


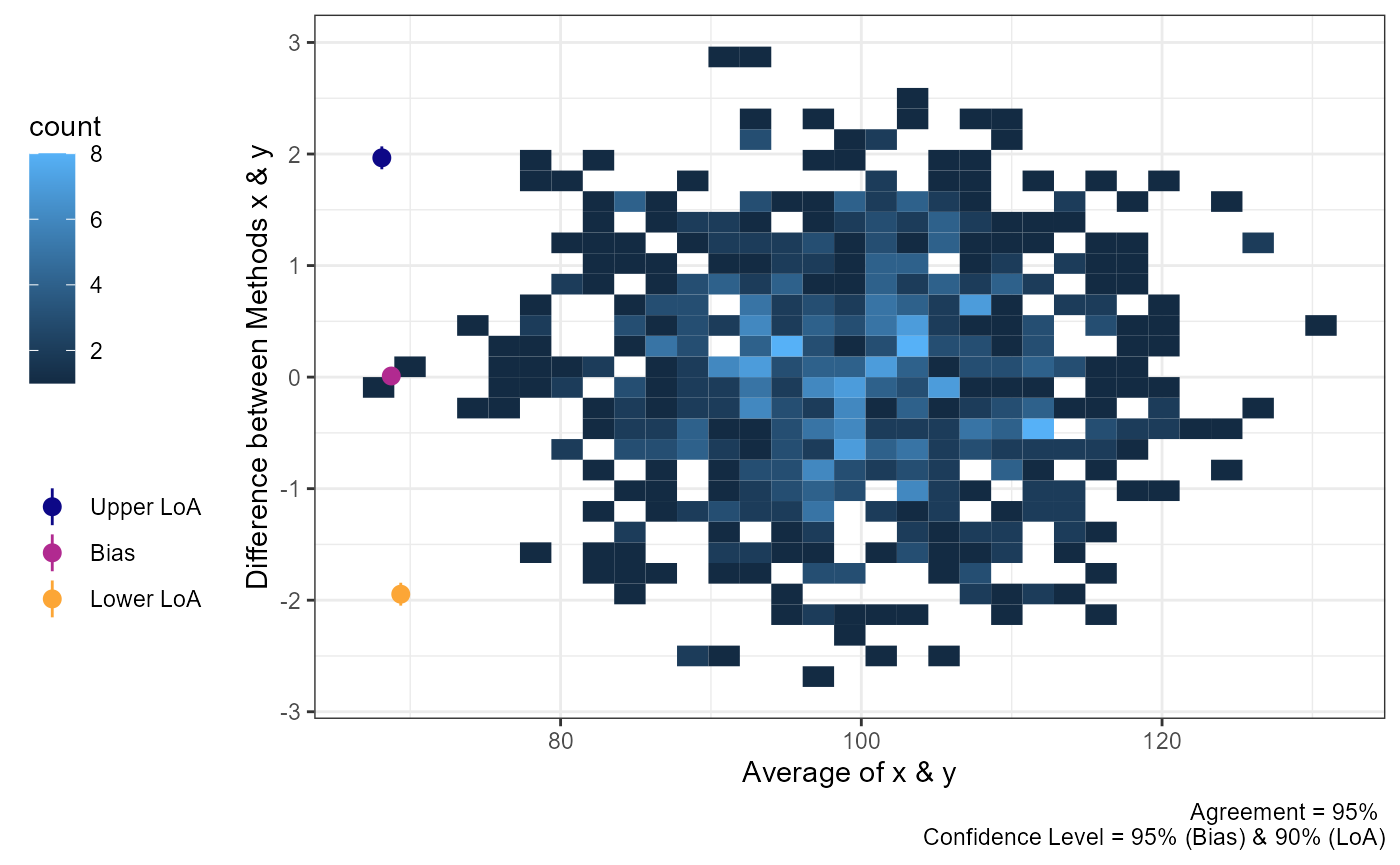
plot(a1,
     geom = "geom_density_2d")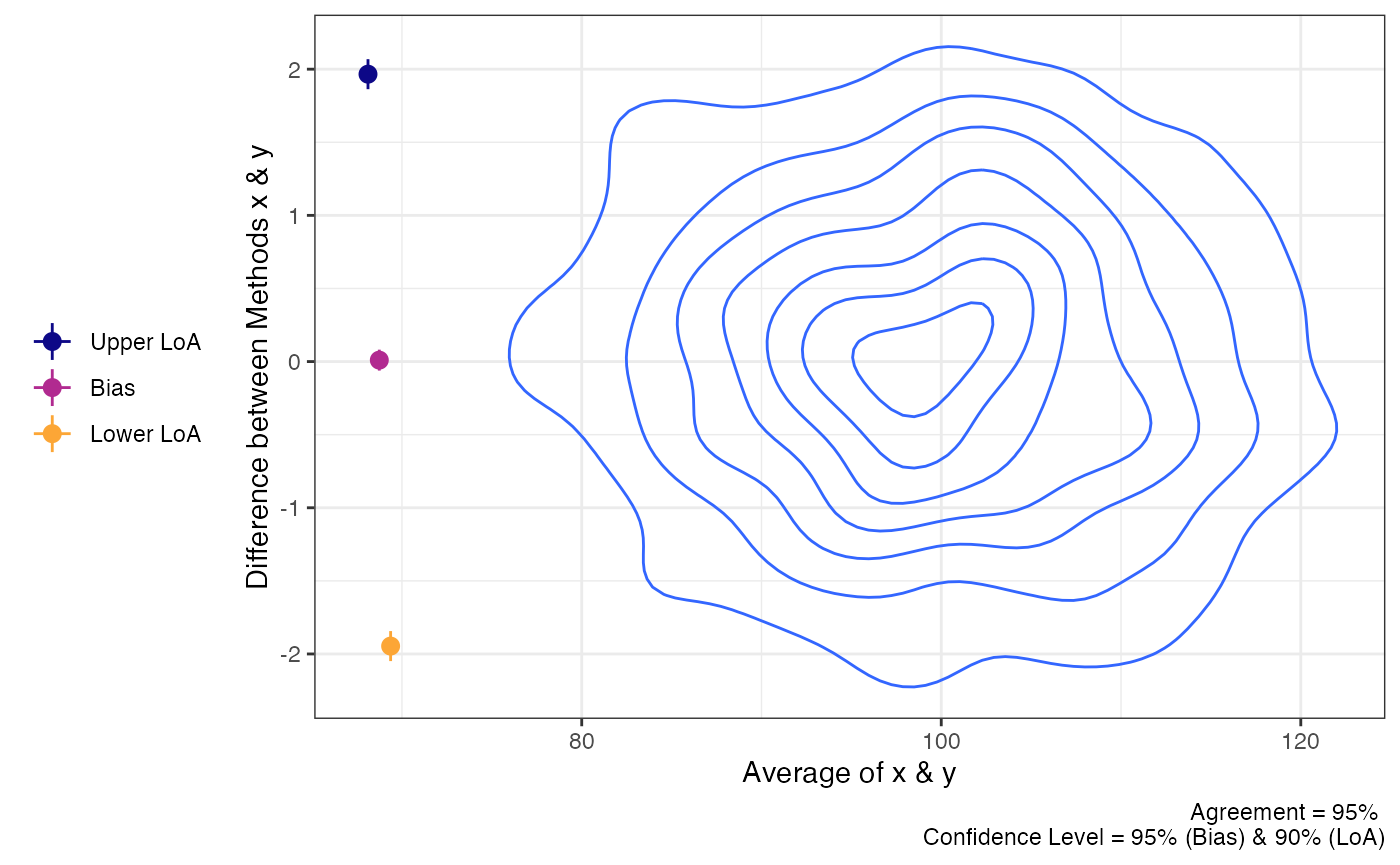


plot(a1,
     geom = "geom_density_2d_filled")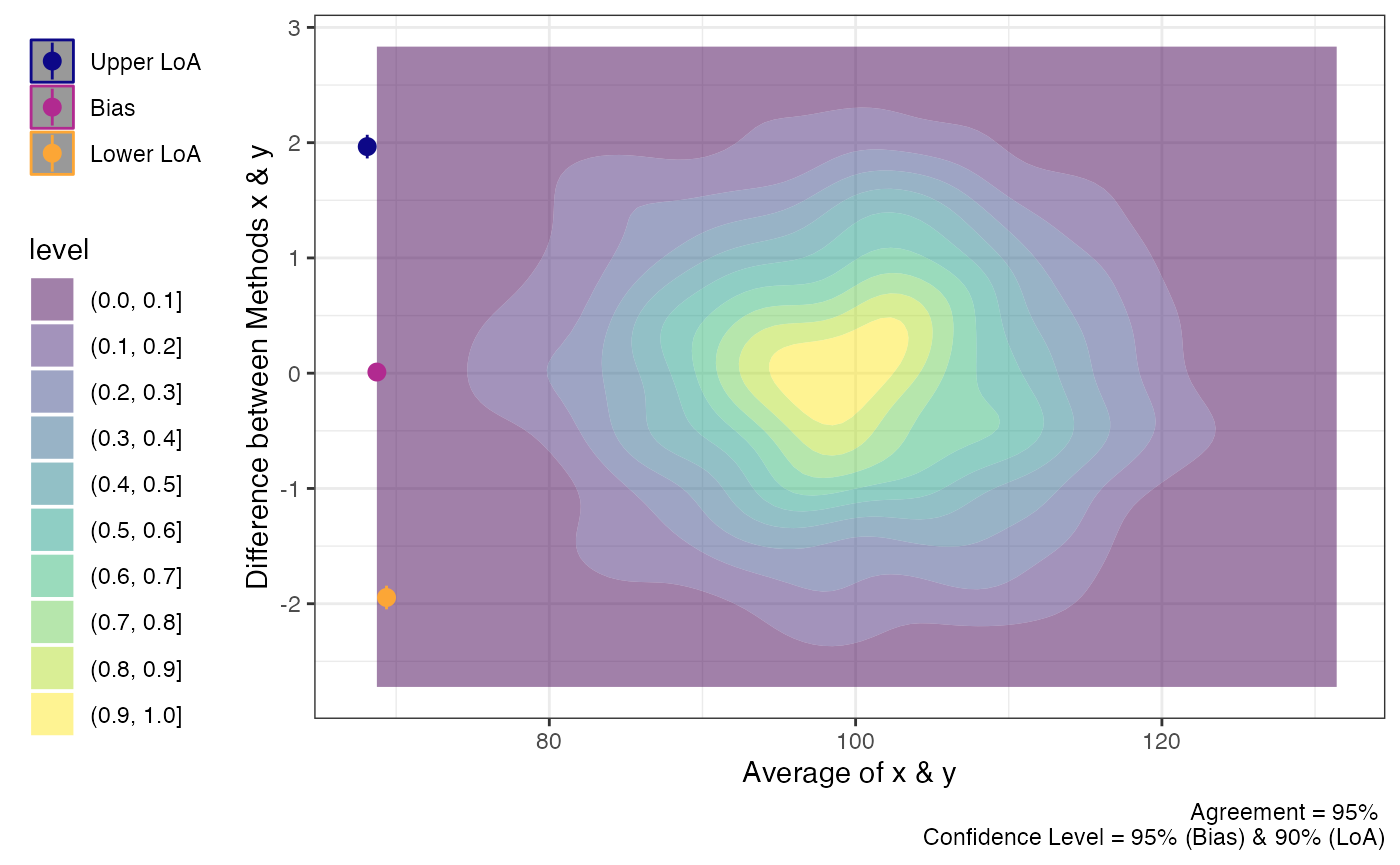


plot(a1,
     geom = "stat_density_2d")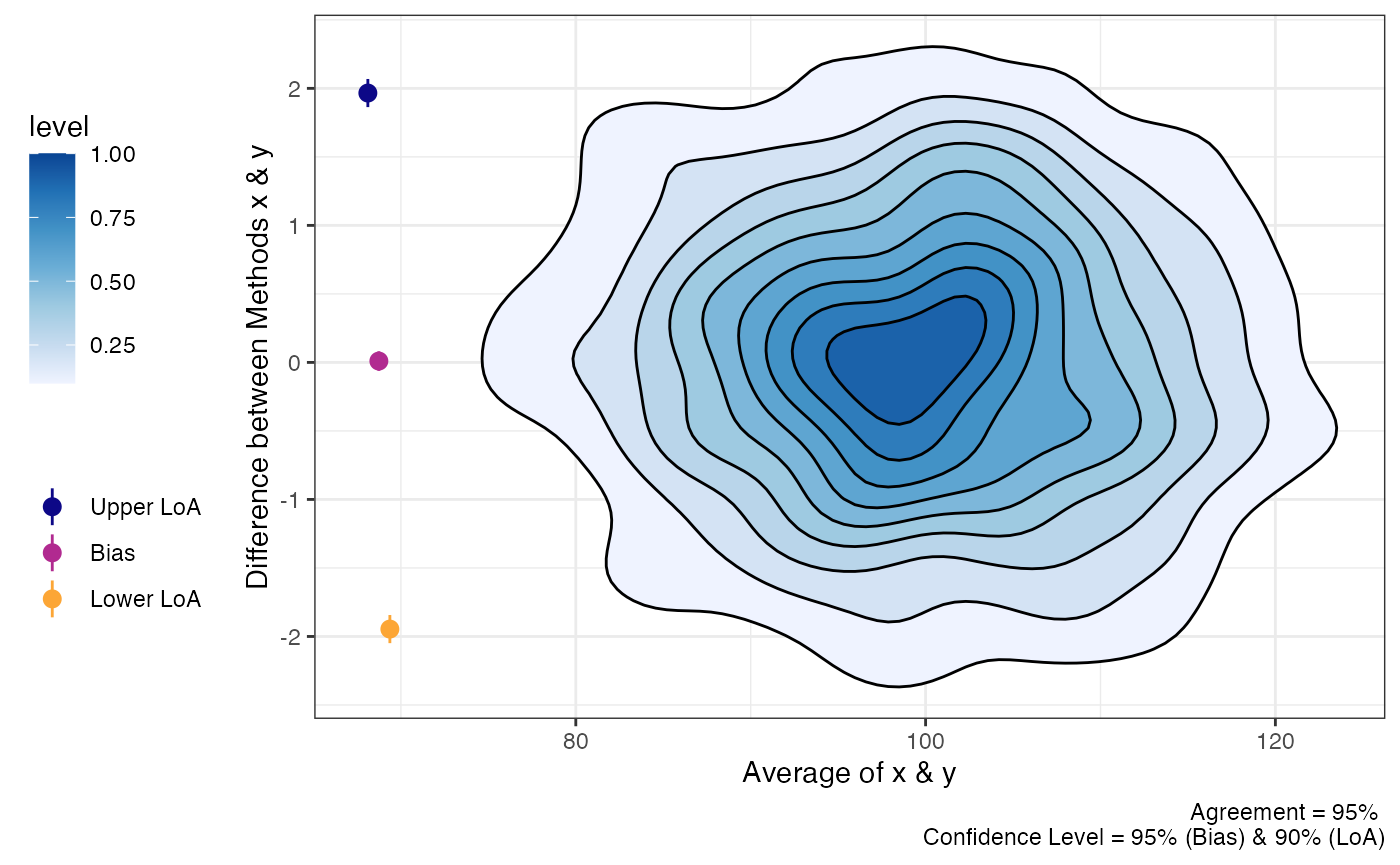

Mixed Models

In some cases, the agreement calculations involve comparing two methods within individuals within varying conditions. For example, the “recpre_long” data set within this package contains two measurements of rectal temperature in 3 different conditions (where there is a fixed effect of condition). For this particular case we can use bootstrapping to estimate the limits of agreement.

The loa_lme function can then calculate the limits of agreement. Like the previous functions, the data set must be set with the data argument. The diff is the column which contains the difference between the two measurements. The condition is the column that indicates the different conditions that the measurements were taken within. The id is the column containing the subject/participant identifier. The final two arguments replicates and type set the requirements for the bootstrapping procedure. Warning: This is a computationally heavy procedure and it may take a few seconds to a few minutes to complete depending the number of replicates or if het_var is set to TRUE.


recpre_long$avg = (recpre_long$PM + recpre_long$PM)/2
a4 = loa_lme(data = recpre_long,
               diff = "diff",
               avg = "avg",
               #condition = "trial_condition",
               id = "id",
               #plot.xaxis = "AM",
               replicates = 199,
               type = "perc")

Power Analysis for Agreement

There are surprisingly few resources for planning a study that attempts to quantify agreement between two methods. Therefore, we have added one function, with hopefully more in the future, to aid in the power analysis for simple agreement studies. The current function is blandPowerCurve which constructs a “curve” of power across sample sizes, agreement levels, and confidence levels. This is based on the work of Lu et al. (2016).

For this function the user must define the hypothesized limits of agreement (delta), mean difference between methods (mu), and the standard deviation of the difference scores (SD). There is also the option of adjusting the range of sample size (default: seq(10,100,1) which is 10 to 100 by 1), the agreement level (default is 95%), and confidence level (default is 95%). The function then produces a data frame of the results. A quick look at the head and we can see that we have low statistical power when the sample size is at the lower end of the range.

power_res <- blandPowerCurve(
  samplesizes = seq(10, 100, 1),
  mu = 0.5,
  SD = 2.5,
  delta = c(6,7),
  conf.level = c(.90,.95),
  agree.level = c(.8,.9)
)

head(power_res)
#>    N  mu  SD delta     power agree.level conf.level
#> 1 10 0.5 2.5     6 0.4870252         0.8        0.9
#> 2 11 0.5 2.5     6 0.5624800         0.8        0.9
#> 3 12 0.5 2.5     6 0.6262736         0.8        0.9
#> 4 13 0.5 2.5     6 0.6802613         0.8        0.9
#> 5 14 0.5 2.5     6 0.7260286         0.8        0.9
#> 6 15 0.5 2.5     6 0.7649104         0.8        0.9

We can then find the sample size at which (or closest to which) a desired power level with the find_n method for powerCurve objects created with the function above.

find_n(power_res, power = .8)
#> # A tibble: 8 × 5
#>   delta conf.level agree.level power     N
#>   <dbl>      <dbl>       <dbl> <dbl> <dbl>
#> 1     6       0.9          0.8 0.798    16
#> 2     6       0.9          0.9 0.802    50
#> 3     6       0.95         0.8 0.798    20
#> 4     6       0.95         0.9 0.802    63
#> 5     7       0.9          0.8 0.847    10
#> 6     7       0.9          0.9 0.800    19
#> 7     7       0.95         0.8 0.775    11
#> 8     7       0.95         0.9 0.806    24

Additionally we can plot the power curve to see how power changes over different levels of delta, agree.level, and conf.level

plot(power_res)

References

Bland, J Martin, and Douglas G Altman. 1986. “Statistical Methods for Assessing Agreement Between Two Methods of Clinical Measurement.” The Lancet 327 (8476): 307–10. https://doi.org/10.1016/s0140-6736(86)90837-8.
———. 1999. “Measuring Agreement in Method Comparison Studies.” Statistical Methods in Medical Research 8 (2): 135–60. https://doi.org/10.1177/096228029900800204.
Carrasco, Josep L., Tonya S. King, and Vernon M. Chinchilli. 2009. “The Concordance Correlation Coefficient for Repeated Measures Estimated by Variance Components.” Journal of Biopharmaceutical Statistics 19 (1): 90–105. https://doi.org/10.1080/10543400802527890.
King, Tonya S, Vernon M Chinchilli, and Josep L Carrasco. 2007. “A Repeated Measures Concordance Correlation Coefficient.” Statistics in Medicine 26 (16): 3095–3113. https://doi.org/10.1002/sim.2778.
Koenker, Roger. 2020. Quantreg: Quantile Regression. https://CRAN.R-project.org/package=quantreg.
Lin, Lawrence I-Kuei. 1989. “A Concordance Correlation Coefficient to Evaluate Reproducibility.” Biometrics 45 (1): 255. https://doi.org/10.2307/2532051.
Lu, Meng-Jie, Wei-Hua Zhong, Yu-Xiu Liu, Hua-Zhang Miao, Yong-Chang Li, and Mu-Huo Ji. 2016. “Sample Size for Assessing Agreement Between Two Methods of Measurement by Bland-Altman Method.” The International Journal of Biostatistics 12 (2). https://doi.org/10.1515/ijb-2015-0039.
Shieh, Gwowen. 2019. “Assessing Agreement Between Two Methods of Quantitative Measurements: Exact Test Procedure and Sample Size Calculation.” Statistics in Biopharmaceutical Research 12 (3): 352–59. https://doi.org/10.1080/19466315.2019.1677495.
Zou, GY. 2011. “Confidence Interval Estimation for the Blandaltman Limits of Agreement with Multiple Observations Per Individual.” Statistical Methods in Medical Research 22 (6): 630–42. https://doi.org/10.1177/0962280211402548.