Reliability Analysis

Aaron R. Caldwell

Last Updated: 2024-10-24

Source: vignettes/reliability_analysis.Rmd

Background

Another feature of this R package is the ability to estimate the reliability of a measurement. This R package allows for the calculation of Intraclass Correlation Coefficients (ICC), various standard errors (SEM, SEE, and SEP), and coefficient of variation. All of the underlying calculations (sans the coefficient of variation) are based on the paper by Weir (2005)1. This is a fairly popular paper within my own field (kinesiology), and hence was the inspiration for creating this function that provides all the calculative approaches included within that manuscript.

Code Demonstration

For this package, the test-retest reliability statistics can be calculated with the reli_stats function. This function allow for data to be input in a long (multiple rows of data for each subject) or in wide (one row for each subject but a column for each item/measure).

For the long data form, the column containing the subject identifier (id), item number (item), and measurements (measure) are provided. In this function I refer to items similar to if we were measuring internal consistency for a questionnaire (which is just a special case of test-retest reliability). So, item could also be refer to time points, which is what is typically seen in human performance settings where test-retest reliability may be evaluated over the course of repeated visits to the same laboratory. If wide is set to TRUE then the columns containing the measurements are provided (e.g., c("value1","value2","value3")).

To demonstrate the function, I will create a data set in the wide format.


  # Example from Shrout and Fleiss (1979), pg. 423
  dat = data.frame(judge1 = 
                     c(9,6,8,7,10,6),
                   judge2 = 
                     c(2,1,4,1,5,2),
                   judge3 = 
                     c(5,3,6,2,6,4),
                   judge4 = 
                     c(8,2,8,6,9,7))

Now, that we have a data set (dat), I can use it in the reli_stats function.

test1 = reli_stats(
  data = dat,
  wide = TRUE,
  col.names = c("judge1", "judge2", "judge3", "judge4")
)

This function also has generic print and plot functions. The output from print provides the coefficient of variation, standard errors, and a table of various intraclass correlation coefficients. Notice the conclusions about the reliability of the measurement here would vary greatly based on the statistic being reported. What statistic you should report is beyond the current vignette, but is heavily detailed in Weir (2005). However, within the table there are columns for model and measures which describe the model that is being used and the what these different ICCs are intended to measure, respectively.

print(test1)
#> 
#> Coefficient of Variation (%):  19.1
#> Standard Error of Measurement (SEM):  1.01
#> Standard Error of the Estimate (SEE):  1.22
#> Standard Error of Prediction (SEP):  1.9
#> 
#> Intraclass Correlation Coefficients with  95 % C.I.
#>            Model         Measures  Type    ICC Lower CI Upper CI
#> 1 one-way random        Agreement  ICC1 0.1657 -0.09672   0.6434
#> 2 two-way random        Agreement  ICC2 0.2898  0.04290   0.6911
#> 3  two-way fixed      Consistency  ICC3 0.7148  0.41184   0.9258
#> 4 one-way random   Avg. Agreement ICC1k 0.4428 -0.54504   0.8783
#> 5 two-way random   Avg. Agreement ICC2k 0.6201  0.15204   0.8995
#> 6  two-way fixed Avg. Consistency ICC3k 0.9093  0.73690   0.9804

Also included in the results is a plot of the measurements across the items (e.g., time points).

plot(test1)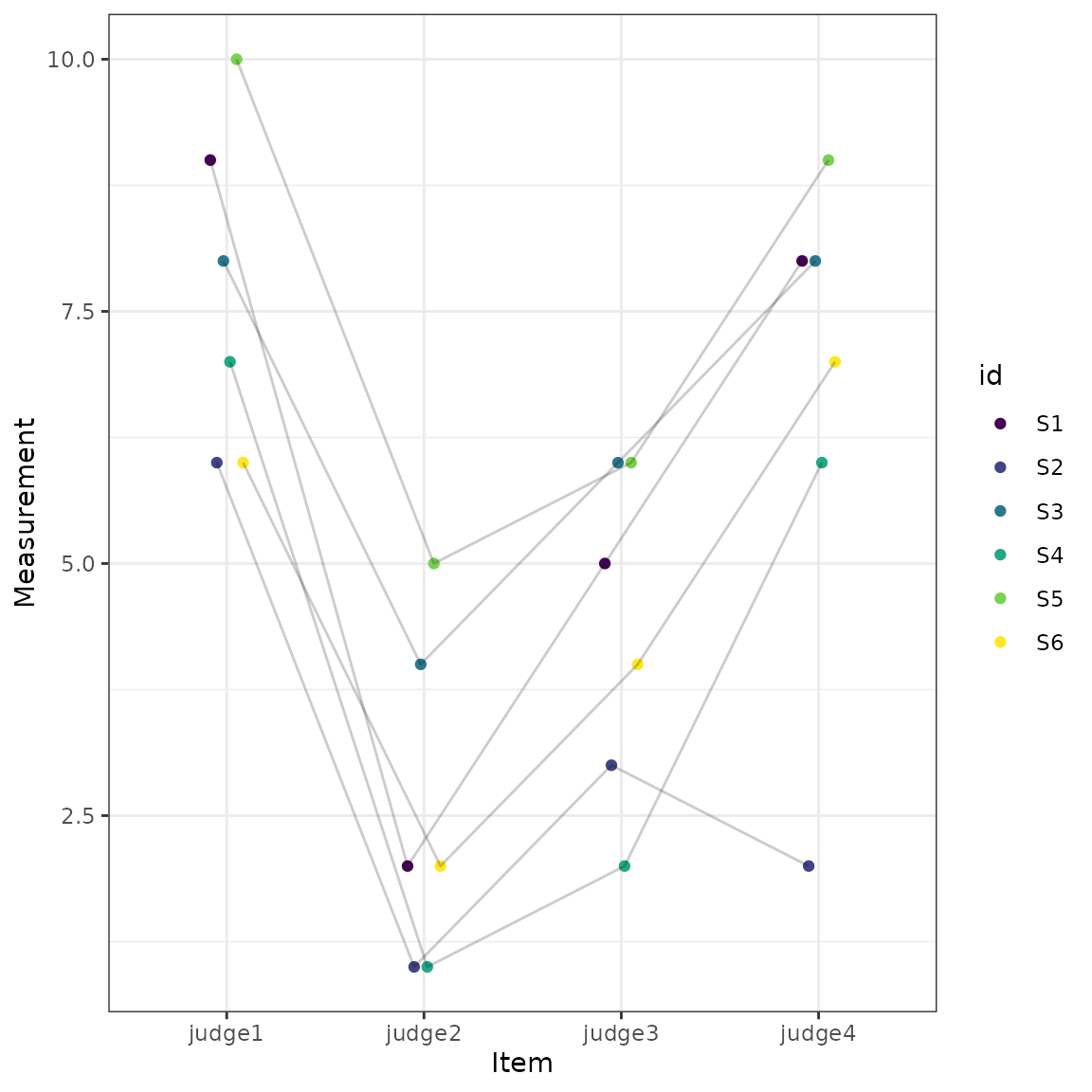

Convergence Issues

In some cases there are convergence issues for the linear mixed models. For this reason, I have added a function, reli_aov, which uses a sums of squares approach (i.e., analysis of variance) rather than a linear mixed model. As you can see below the results will often match that of reli_stats. The only time this function is necessary to use is when there are convergence issues. Rows with missing data are dropped when using reli_aov.

test2 = reli_aov(
  data = dat,
  wide = TRUE,
  col.names = c("judge1", "judge2", "judge3", "judge4")
)

test2
#> 
#> Coefficient of Variation (%):  19.1
#> Standard Error of Measurement (SEM):  1.01
#> Standard Error of the Estimate (SEE):  1.22
#> Standard Error of Prediction (SEP):  1.9
#> 
#> Intraclass Correlation Coefficients with  95 % C.I.
#>            Model         Measures  Type    ICC Lower CI Upper CI
#> 1 one-way random        Agreement  ICC1 0.1657 -0.09672   0.6434
#> 2 two-way random        Agreement  ICC2 0.2898  0.04290   0.6911
#> 3  two-way fixed      Consistency  ICC3 0.7148  0.41183   0.9258
#> 4 one-way random   Avg. Agreement ICC1k 0.4428 -0.54504   0.8783
#> 5 two-way random   Avg. Agreement ICC2k 0.6201  0.15204   0.8995
#> 6  two-way fixed Avg. Consistency ICC3k 0.9093  0.73690   0.9804

Calculative Approach

Model

The linear mixed model used for the calculations is specified as the following:

Yi∼N(αj[i],k[i],σ2) Y_{i} \sim\ N \left(\alpha_{j[i],k[i]}, \sigma^2 \right)

αj∼N(μαj,σαj2), for id j = 1,…,J \alpha_{j} \sim\ N \left(\mu_{\alpha_{j}}, \sigma^2_{\alpha_{j}} \right) \text{, for id j = 1,} \dots \text{,J}

αk∼N(μαk,σαk2), for items k = 1,…,K \alpha_{k} \sim\ N \left(\mu_{\alpha_{k}}, \sigma^2_{\alpha_{k}} \right) \text{, for items k = 1,} \dots \text{,K}

Components of Variance

Mean Squared Error (MSE)

MSE=σ2 MSE = \sigma^2

Variance Between Subjects

MSB=nk⋅σαj2+σ2 MSB = n_k \cdot \sigma^2_{\alpha j} + \sigma^2

Variance Between Items/Judges

MSJ=nj⋅σαk2+σ2 MSJ = n_{j} \cdot \sigma^2_{\alpha_{k}} + \sigma^2

Variance Within Subjects/Participants

MSW=σ2+σαk2 MSW = \sigma^2 + \sigma^2_{\alpha_{k}}

Intraclass Correlation Coefficients

ICC(1,1)=MSB−MSWMSB+(nj−1)⋅MSW ICC_{(1,1)} = \frac{MSB - MSW}{MSB + (n_j-1) \cdot MSW} ICC(2,1)=MSB−MSEMSB+(nj−1)⋅MSE+nj⋅(MSJ−MSE)⋅n−1 ICC_{(2,1)} = \frac{MSB - MSE}{MSB+(n_j -1) \cdot MSE + n_j \cdot (MSJ - MSE) \cdot n^{-1}} ICC(3,1)=MSB−MSEMSB+(nj−1)⋅MSE ICC(_{3,1)} = \frac{MSB - MSE}{MSB + (n_j -1) \cdot MSE} ICC(1,k)=MSB−MSWMSB ICC_{(1,k)} = \frac{MSB - MSW}{MSB} ICC(2,k)=MSB−MSWMSB+(MSJ−MSE)⋅nj−1 ICC_{(2,k)} = \frac{MSB - MSW}{MSB + (MSJ - MSE) \cdot n_j^{-1}} ICC(3,k)=MSB−MSEMSB ICC_{(3,k)} = \frac{MSB - MSE}{MSB}

ICC Confidence Intervals

ICC(1,1)

F=MSBMSW F = \frac{MSB}{MSW}

dfn=nj−1 df_{n} = n_j - 1

dfd=nj⋅(nk−1) df_{d} = n_j \cdot (n_k - 1)

$$ F_{L} = \frac{F}{F_{(1 - \alpha, \space df_{n}, \space df_{d})}} $$

$$ F_{U} = F \cdot F_{(1 - \alpha, \space df_{d}, \space df_{n})} $$

$$ Lower \space CI = \frac{(F_L - 1)}{(F_L + (n_j - 1))} $$

$$ Upper \space CI = \frac{(F_U - 1)}{(F_U + n_j - 1)} $$

ICC(2,1)

F=MSJMSE F = \frac{MSJ}{MSE}

vn=(nk−1)⋅(nj−1)⋅[(nj⋅ICC(2,1)⋅F+nj⋅(1+(nk−1)⋅ICC(2,1))−nk⋅ICC(2,1))]2 vn = (n_k - 1) \cdot (n_j - 1) \cdot [(nj \cdot ICC_{(2,1)} \cdot F + n_j \cdot (1 + (n_k - 1) \cdot ICC_{(2,1)}) - n_k \cdot ICC_{(2,1)})]^2

vd=(nj−1)⋅nk2⋅ICC(2,1)2⋅F2+(nj⋅(1+(nk−1)⋅ICC(2,1))−nk⋅ICC(2,1))2 vd = (n_j - 1) \cdot n_k^2 \cdot ICC_{(2,1)}^2 \cdot F^2 + (n_j \cdot (1 + (n_k - 1) \cdot ICC_{(2,1)}) - n_k \cdot ICC_{(2,1)})^2 v=vnvd v = \frac{vn}{vd}

$$ F_{L} = F_{(1 - \alpha, \space n_j-1, \space v)} $$

$$ F_{U} = F_{(1 - \alpha, \space v, \space n_j - 1)} $$

$$ Lower \space CI = \frac{n_j \cdot (MSB - F_U \cdot MSE)}{(F_U \cdot (n_k \cdot MSJ + (n_k \cdot n_j - n_k - n_j) \cdot MSE) + n_j \cdot MSB)} $$

$$ Upper \space CI = \frac{n_j \cdot (MSB \cdot F_L - MSE)}{(n_k \cdot MSJ + (n_k \cdot n_j - n_k - n_j) \cdot MSE + n_j \cdot F_L \cdot MSB)} $$

ICC(3,1)

F=MSJMSE F = \frac{MSJ}{MSE} dfn=nj−1 df_{n} = n_j - 1 dfd=(nj−1)⋅(nk−1) df_{d} = (n_j-1) \cdot (n_k - 1)

$$ F_{L} = \frac{F}{F_{(1 - \alpha, \space df_{n}, \space df_{d})}} $$ $$ F_{U} = F \cdot F_{(1 - \alpha, \space df_{n}, \space df_{d})} $$ F3L<−F31/qf(1−alpha,df21n,df21d) F3L <- F31/qf(1 - alpha, df21n, df21d) F3U<−F31*qf(1−alpha,df21d,df21n) F3U <- F31 * qf(1 - alpha, df21d, df21n) $$ Lower \space CI = (F3L - 1)/(F3L + n_k - 1) $$

$$ Upper \space CI = (F3U - 1)/(F3U + n_k - 1) $$

ICC(1,k)

F=MSB−MSWMSB F = \frac{MSB - MSW}{MSB} dfn=nj−1 df_{n} = n_j - 1

dfd=nj⋅(nk−1) df_{d} = n_j \cdot (n_k - 1)

$$ F_{L} = \frac{F}{F_{(1 - \alpha, \space df_{n}, \space df_{d})}} $$ $$ F_{U} = F \cdot F_{(1 - \alpha, \space df_{d}, \space df_{n})} $$

$$ Lower \space CI = 1-\frac{1}{F_L} $$ $$ Upper \space CI = 1-\frac{1}{F_U} $$

ICC(2,k)

F=MSB−MSWMSB F = \frac{MSB - MSW}{MSB}

vn=(nk−1)⋅(nj−1)⋅[(nj⋅ICC(2,k)⋅F+nj⋅(1+(nk−1)⋅ICC(2,k))−nk⋅ICC(2,k))]2 vn = (n_k - 1) \cdot (n_j - 1) \cdot [(nj \cdot ICC_{(2,k)} \cdot F + n_j \cdot (1 + (n_k - 1) \cdot ICC_{(2,k)}) - n_k \cdot ICC_{(2,k)})]^2

vd=(nj−1)⋅nk2⋅ICC(2,k)2⋅F2+(nj⋅(1+(nk−1)⋅ICC(2,k))−nk⋅ICC(2,k))2 vd = (n_j - 1) \cdot n_k^2 \cdot ICC_{(2,k)}^2 \cdot F^2 + (n_j \cdot (1 + (n_k - 1) \cdot ICC_{(2,k)}) - n_k \cdot ICC_{(2,k)})^2

v=vnvd v = \frac{vn}{vd}

$$ F_{L} = F_{(1 - \alpha, \space n_j-1, \space v)} $$ $$ F_{U} = F_{(1 - \alpha, \space v, \space n_j - 1)} $$

L3=nj⋅(MSB−FU⋅MSE)(FU⋅(nk⋅MSJ+(nk⋅nj−nk−nj)⋅MSE)+nj⋅MSB) L3 = \frac{n_j \cdot (MSB - F_U \cdot MSE)}{(F_U \cdot (n_k \cdot MSJ + (n_k \cdot n_j - n_k - n_j) \cdot MSE) + n_j \cdot MSB)}

U3=nj⋅(MSB⋅FL−MSE)(nk⋅MSJ+(nk⋅nj−nk−nj)⋅MSE+nj⋅FL⋅MSB) U3 = \frac{n_j \cdot (MSB \cdot F_L - MSE)}{(n_k \cdot MSJ + (n_k \cdot n_j - n_k - n_j) \cdot MSE + n_j \cdot F_L \cdot MSB)}

$$ Lower \space CI = \frac{L3 \cdot n_k}{(1 + L3 \cdot (n_k - 1))} $$

$$ Upper \space CI = \frac{U3 \cdot n_k}{(1 + U3 \cdot (n_k - 1))} $$

ICC(3,k)

F=MSBMSE F = \frac{MSB}{MSE}

dfn=nj−1 df_n = n_j - 1

dfd=(nj−1)⋅(nk−1) df_d = (n_j - 1) \cdot (n_k - 1)

$$ F_L = \frac{F}{F_{(1 - \alpha, \space df_n, \space df_d})} $$

$$ F_U = F \cdot F_{(1 - \alpha, \space df_d, \space df_n)} $$

$$ Lower \space CI = 1-\frac{1}{F_L} $$

$$ Upper \space CI = 1-\frac{1}{F_U} $$

Standard Error Calculations

The standard error of the measurement (SEM), standard error of the estimate (SEE), and standard error of prediction (SEP) are all estimated with the following calculations.2

The default SEM calculation is the following:

SEM=MSE SEM = \sqrt{MSE} Alternatively, the SEM can be calculated as the following and the ICC is determined through the se_type argument:

SEM=SStotal(N−1)⋅1−ICC SEM = \sqrt{\frac{SS_{total}}{(N-1)}} \cdot \sqrt{1-ICC} The other measures default to using the following equations. The default is to use ICC3,1ICC_{3,1}, but can be modified with the se_type argument.

SEE=SStotal(N−1)⋅ICC⋅(1−ICC) SEE = \sqrt{\frac{SS_{total}}{(N-1)}} \cdot \sqrt{ICC \cdot (1-ICC)}

SEP=SStotal(N−1)⋅1−ICC2 SEP = \sqrt{\frac{SS_{total}}{(N-1)}} \cdot \sqrt{1-ICC^2}

Coefficient of Variation

The CV is calculated 3 potential ways within reli_stats. I highly recommend reporting the default version of CV.

  1. From the MSE (default)

CV=MSEy‾ CV = \frac{ \sqrt{MSE} }{ \bar y}

  1. From the SEM3

CV=SEMy‾ CV = \frac{SEM}{ \bar y}

  1. From the model residuals (most liberal)

CV=Σi=1N(yi−ŷi)2Nobsy‾ CV = \frac{\sqrt{\frac{\Sigma^{N}_{i=1}(y_i - \hat y_i)^2}{N_{obs}}}}{ \bar y}

Other Confidence Intervals

If the other_ci argument is set to TRUE then confidence intervals will be calculated for the CV, SEM, SEP, and SEE.

Chi-square

The default method is type = 'chisq. This method utilizes the chi-square distribution to approximate confidence intervals for these measurements. The accuracy of these estimates is likely variable, and is probably poor for small samples.

For the CV, the calculation is as follows:

$$ Lower \space CI = \frac{CV}{\sqrt{(\frac{\chi^2_{1-\alpha/2}}{df_{error}+1}-1) \cdot CV^2 \cdot \frac{\chi^2_{1-\alpha/2}}{df_{error}}}} $$

$$ Upper \space CI = \frac{CV}{\sqrt{(\frac{\chi^2_{\alpha/2}}{df_{error}+1}-1) \cdot CV^2 \cdot \frac{\chi^2_{\alpha/2}}{df_{error}}}} $$ For the variance based measures (s) the calculation is as follows:

$$ Lower \space CI = s \cdot \sqrt{\frac{df_{error}}{\chi^2_{1-\alpha/2}}} $$

$$ Upper \space CI = s \cdot \sqrt{\frac{df_{error}}{\chi^2_{\alpha/2}}} $$

Bootstrap

If type is not set to chisq then bootstrapping is performed.

  1. reli_aov utilizes a non-parametric ordinary bootstrap.
  2. reli_stats utilizes a parametric bootstrap.

The number of resamples can be set with the replicates argument (default is 1999; increase for greater accuracy or lower for greater speed). The reported confidence intervals are estimated using the percentile method type = 'perc', the normal type = 'norm', or basic methods type = 'basic'.

To ensure reproducibility, please use set.seed() when these confidence intervals are calculated.

Inter-Rater Reliability

In some cases, the reliability of a categorical or ordinal scale may be worth investigating. For example, physicians may want to develop a diagnosis tool and ensure that the diagnosis is reliable (i.e., categorical designation) or severity of the disease (i.e., a Likert-type scale). Coefficients can be calculated to assess the degree of inter-rater reliability. In its simplest form, the percent agreement between all the raters can be calculated. All other coefficients of agreement are essentially trying to “correct” for random guessing of the rater. The function to make these calculations in the SimplyAgree is agree_coef, and it produces 4 estimates: percent agreement, Gwet’s AC, Fleiss’ Kappa, and Krippendorff’s Alpha. However, other packages provide much a much greater breadth of calculative approaches (Gwet 2019).

In the agree_coef function, the user can specify weighted = TRUE. If this argument is set to true than the ratings have quadratic weights applied to them. Essentially, this penalizes values farther away from each other more than those close to each other. For example, a pair of values equal to 3 and 4 would be penalized less than a pair of values to 1 and 4. For more details, on these “agreement coefficients” I refer all users to Gwet’s textbook on inter-rater agreement (Gwet 2014).

As a demonstration, we can create a matrix of ratings.

  ratermat1 = ("Rater1 Rater2 Rater3 Rater4
1       1      1     NA      1
2       2      2      3      2
3       3      3      3      3
4       3      3      3      3
5       2      2      2      2
6       1      2      3      4
7       4      4      4      4
8       1      1      2      1
9       2      2      2      2
10     NA      5      5      5
11     NA     NA      1      1
12     NA     NA      3     NA")

  ratermat2 = as.matrix(read.table(textConnection(ratermat1),
                       header=TRUE,
                       row.names=1))

We can then perform the analysis without the weights.

agree_coef(data = ratermat2,
                     wide = TRUE,
                     weighted = FALSE,
                     col.names = c("Rater1", "Rater2", "Rater3", "Rater4"))
#>                              est        se  lower.ci upper.ci
#> Percent Agreement      0.8181818 0.1256090 0.5417184        1
#> Gwet's AC1             0.7754441 0.1429500 0.4608133        1
#> Fleiss' Kappa          0.7611693 0.1530192 0.4243763        1
#> Kririppendorff's Alpha 0.7434211 0.1454787 0.4192743        1

Or, perform it with weighting.

agree_coef(data = ratermat2,
                    wide = TRUE,
                    weighted = TRUE,
                    col.names = c("Rater1", "Rater2", "Rater3", "Rater4"))
#>                              est         se  lower.ci upper.ci
#> Percent Agreement      0.9753788 0.09061628 0.7759337        1
#> Gwet's AC2             0.9140007 0.10396224 0.6851814        1
#> Fleiss' Kappa          0.8649351 0.14603361 0.5435173        1
#> Kririppendorff's Alpha 0.8491071 0.12905120 0.5615632        1

References

Gwet, Kilem L. 2014. Handbook of Inter-Rater Reliability. Advanced Analytics, LLC. https://www.agreestat.com/book4/.
———. 2019. irrCAC: Computing Chance-Corrected Agreement Coefficients (CAC). https://CRAN.R-project.org/package=irrCAC.
McGraw, Kenneth O, and Seok P Wong. 1996. “Forming Inferences about Some Intraclass Correlation Coefficients.” Psychological Methods 1 (1): 30. https://doi.org/10.1037/1082-989X.1.1.30.
Shrout, Patrick E, and Joseph L Fleiss. 1979. “Intraclass Correlations: Uses in Assessing Rater Reliability.” Psychological Bulletin 86 (2): 420. https://doi.org/10.1037/0033-2909.86.2.420.
Weir, Joseph P. 2005. “Quantifying Test-Retest Reliability Using the Intraclass Correlation Coefficient and the SEM.” The Journal of Strength and Conditioning Research 19 (1): 231. https://pubmed.ncbi.nlm.nih.gov/15705040/.

  1. The paper by Weir also appears to heavily rely on the work of Shrout and Fleiss (1979) and McGraw and Wong (1996)↩︎

  2. This section was previously incorrect. The variance calculation used to utilize njn_j instead of N.↩︎

  3. Also called “%SEM” in some texts. Equivalent to MSE if the se_type is set to “MSE”↩︎