Agreement & Tolerance Limits

Aaron R. Caldwell

Last Updated: 2024-10-24

Source: vignettes/agreement_analysis.Rmd

In this vignette I will briefly demonstrate how SimplyAgree calculates agreement and tolerance limits. This vignette assumes the reader has some familiarity with “limits of agreement” (Bland-Altman limits) and is familiar with the concept of prediction intervals. Please read the references listed in this vignette before going further if you are not familiar with both concepts.

Agree or Tolerate?

Francq, Berger, and Boachie (2020) pose this question in a paper published in Statistics in Medicine. Traditionally, those working in medicine or physiology have defaulted to calculating some form of “limits of agreement” that Bland and Altman (1986) recommended in their seminal paper. The recommendation by Bland and Altman (1986) was only an approximation, and that has undergone many modifications (e.g., Bland and Altman 1999; Zou 2011) to improve the accuracy of the agreement interval and their associated confidence intervals. Meanwhile, the field of industrial statistics has focused on calculating tolerance limits. There are R packages, such as the tolerance R package available on CRAN, that are entirely dedicated to calculating tolerance limits. It is important to note that tolerance is not limited to the normal distribution and can be applied to other distributions (please see the tolerance package by Young (2010) for more details). However, in the agreement studies typically seen in medicine, tolerance limits may be a more accurate way of determining whether two measurements are adequately close to one another.

To quote Francq, Berger, and Boachie (2020):

In terms of terminology, tolerance means, in this context, that some difference between the methods is tolerated (the measurements are still comparable in practice). Furthermore, the tolerance interval is exact and therefore more appropriate than the agreement interval.

In this package, tolerance limits refer to the “tolerance” associated with the prediction interval for the difference between 2 measurements. The calculative approach (detailed much further below) involves calculating the prediction interval for the difference between two methods (i.e., an estimate of an interval in which a future observation will fall, with a certain probability, given what has already been observed) and then calculating the confidence in the interval (i.e., tolerance). Therefore, if we want a 95% prediction interval with 95% tolerance limits, we are calculating the interval in which 95% of future observations (prediction) with only a 5% probability (1-tolerance) the “true” prediction interval limits are greater/less than the upper/lower tolerance limits.

Personally, I find the use of prediction intervals and tolerance limits more attractive for 2 reasons: 1) the coverage of the prediction intervals and their tolerance limits is often better than confidence intervals for agreement limits, and 2) the interpretation of the tolerance limits is much clearer. For a greater discussion of this topic, please see the manuscript by Francq, Berger, and Boachie (2020) and check out their R package BivRegBLS.

Tolerance

In SimplyAgree we utilize a generalized least square (GLS) model to estimate the prediction interval and tolerance limits. The function uses the gls function from the nlme R package to build the model. This allows a very flexible approach for estimating prediction intervals and tolerance limits.

We can use the tolerance_limits function demonstrate the basic calculations. In this example (below), we use the temps data set to measure the differences between esophageal and rectal temperatures between different times of day (tod) and controlling for the intra-subject correlation.

tolerance_limit(
  data = temps,
  x = "trec_pre", # First measure
  y = "teso_pre", # Second measure
  id = "id", # Subject ID
  condition = "tod", # Identify condition that may affect differences
  cor_type = "sym" # Set correlation structure as Compound Symmetry
)
#> Agreement between Measures (Difference: x-y)
#> 95% Prediction Interval with 95% Tolerance Limits
#> 
#>  Condition   Bias          Bias CI Prediction Interval  Tolerance Limits
#>         AM 0.1537 [0.0595, 0.2479]    [-0.292, 0.5993] [-0.4983, 0.8056]
#>         PM 0.2280 [0.1341, 0.3219]   [-0.3163, 0.7723] [-0.6985, 1.1545]

Calculative Approach

Overall, the model is fit using the gls function, and, for those interested, I would suggest reading book by Pinheiro and Bates which details the function1. This function is different than the linear, or linear mixed, models that are utilized in calculating limits of agreement because it accommodates correlated errors and/or unequal variances.

Arguments Influencing the Model

There are a number of options with the arguments provided in the tolerance_limit function. The only required arguments are x, y, and data which dictate the data frame, and the columns that contain the 2 measurements. The id argument, when specified, identifies the column that contains the subject identifier or some time of nesting within which the data should be correlated to some degree. The time, argument is utilized when the data come from a repeated measures or time series data, and indicates the order of the data points. The condition argument identifies some factor within a data frame that may effect the mean difference (and variance) of the differences between the 2 measurements. The cor_type argument can also be utilized to specific 1 of 3 possible correlation structure types. Lastly, savvy users can specify a particular variance or correlation structure using the weights and correlation arguments which directly alter the model being fit using gls.

Prediction

After the model is fit, the estimated marginal means (EMM), and their associated standard errors (SEM), are calculated based on the gls fit model using emmeans. The standard error of prediction (SEP) for each EMM is then calculated using the SEM and residual standard error from the model (formula below).

SEP=SEM2+Sresidual2 SEP = \sqrt{SEM^2 + S^2_{residual} }

After the SEP is calculated, the prediction interval can be calculated with following:

PI=EMM±t1−α/2,df⋅SEP PI = EMM \pm t_{1-\alpha/2, df} \cdot SEP

NOTE: the degrees of freedom (df) are calculated using an approximation of Satterthwaite (1946) (see Kuznetsova, Brockhoff, and Christensen (2017) for an explanation of this implementation in R).

Tolerance

The type of tolerance limit calculation can be set using the tol_method argument with options including “approx” and “perc”. Tolerance limits are calculated either through the “Beta expectation” approximation (tol_method = "approx") detailed by Francq, Berger, and Boachie (2020) or through a parametric bootstrap method (tol_method = "perc"). The bootstrap methods re-samples from the model and, after a certain number of replicates (default is 1999), calculates the bounds the prediction interval based on the quantiles of the replicates for the lower and upper limit. This is preferred for its accuracy and power, but is extremely slow which may involve computations lasting greater than 2 minutes for even small data sets. The approximation is the default only because it is substantially quicker. Users should be aware that the bootstrap method will likely be more accurate and provide smaller (i.e., more forgiving) tolerance limits.

The approximate tolerance limits based on the work of Francq, Berger, and Boachie (2020) are calculated as the following:

TI=EMM±z1−α1/2⋅SEP⋅dfχα2,df2 TI = EMM \pm z_{1-\alpha_1/2} \cdot SEP \cdot \sqrt{\frac{df}{\chi^2_{\alpha_2,df}}} NOTE: α1\alpha_1 refers to the alpha-level for the prediction interval (modified by the pred_level argument; 1-pred_level) whereas α2\alpha_2 refers to the alpha-level for the tolerance limit (modified by the tol_level argument; 1-tol_level).

Example

In the temps data we have different measures of core temperature at varying times of day. Let us assume we want to measure pre-exercise agreement between esophageal and rectal temperature while controlling for time of day (tod).

test1 = tolerance_limit(data = temps,
                        x = "teso_pre",
                        y = "trec_pre",
                        id = "id",
                        condition = "tod")

test1
#> Agreement between Measures (Difference: x-y)
#> 95% Prediction Interval with 95% Tolerance Limits
#> 
#>  Condition    Bias            Bias CI Prediction Interval  Tolerance Limits
#>         AM -0.1537 [-0.2479, -0.0595]    [-0.5993, 0.292] [-0.8056, 0.4983]
#>         PM -0.2280 [-0.3219, -0.1341]   [-0.7723, 0.3163] [-1.1545, 0.6985]

Agreement

The agreement limit calculations in SimplyAgree are a tad more constrained than the tolerance limit. There are only 3 types of calculations that can be made: simple, replicate, and nested. The simple calculation each pair of observations (x and y) are independent; meaning that each pair represents one subject/participant. Sometimes there are multiple measurements taken within subjects when comparing two measurements tools. In some cases the true underlying value will not be expected to vary (i.e., replicates or “reps”), or multiple measurements may be taken within an individual and these values are expected to vary (i.e., nested).

The agreement_limit function, unlike the other agreement functions in the package (i.e., agree_test, agree_reps, and agree_nest), allows users to make any of the three calculations all-in-one function. Further, agreement_limit assumes you are only interested in the outermost confidence interval of the limits of agreement and therefore one-tailed confidence intervals are only calculated for the LoA (i.e., there is no TOST argument).

Arguments Influencing the LoA Calculations

Users of the this function have a number of options. The only required arguments are x, y, and data which dictate the data frame, and the columns that contain the 2 measurements. The id argument, when specified, identifies the column that contains the subject identifier. This is only necessary if it is a replicate or nested design. The type of design is dictated by data_type argument. Additionally, the loa_calc function dictates how the limits of agreement are calculated. Users have the option of computing Bland and Altman (1999) or MOVER (Zou 2011; Donner and Zou 2012) limits of agreement (calculations detailed below). I strongly recommend utilizing the MOVER limits of agreement over the Bland-Altman limits (Zou 2011; Donner and Zou 2012) as it is the more conservative of the two options.

Simple Agreement

In the simplest scenario, a study may be conducted to compare one measure (e.g., x) and another (e.g., y). In this scenario each pair of observations (x and y) are independent; that means that each pair represents one subject/participant that is uncorrelated with other pairs.

The data for the two measurements are put into the x and y arguments.

# Calc. LoA
a1 = agreement_limit(data = reps,
                     x = "x",
                     y = "y")
# print
a1
#> MOVER Limits of Agreement (LoA)
#> 95% LoA @ 5% Alpha-Level
#> Independent Data Points
#> 
#>    Bias           Bias CI Lower LoA Upper LoA            LoA CI
#>  0.4383 [-0.1669, 1.0436]    -1.947     2.824 [-3.0117, 3.8884]
#> 
#> SD of Differences = 1.217

Calculation Steps

The reported limits of agreement are derived from the work of Bland and Altman (1986) and Bland and Altman (1999).

LoA

LoA=d‾±z1−(1−agree)/2⋅Sd LoA = \bar d \pm z_{1-(1-agree)/2} \cdot S_d

wherein z1−(1−agree)/2z_{1-(1-agree)/2} is the value of the normal distribution at the given agreement level (default is 95%), d‾\bar d is the mean of the differences, and SdS_d is the standard deviations of the differences.

Confidence Interval

  1. Calculate variance of LoA

SLoA=Sd⋅1N+z1−(1−agree)/222⋅(N−1) S_{LoA} = S_d \cdot \sqrt{\frac{1}{N}+ \frac{z^2_{1-(1-agree)/2}}{2 \cdot(N-1)} }

  1. Calculate Left Moving Estimator

Bland-Altman Method

$$ LME = t_{1 - \alpha, \space df} \cdot S_{LoA} $$ MOVER Method

LME=Sd⋅z1−α2N+z1−agree2⋅(dfχα,df2−1)2 LME = S_d \cdot \sqrt{\frac{z_{1-\alpha}^2}{N} + z^2_{1-agree} \cdot (\sqrt{\frac{df}{\chi^2_{\alpha,df}}}-1)^2}

  1. Calculate Confidence Interval

$$ Lower \space LoA \space C.I. = Lower \space LoA - LME $$

$$ Upper \space LoA \space C.I. = Upper \space LoA + LME $$

Repeated Measures Agreement

In many cases there are multiple measurements taken within subjects when comparing two measurements tools. In some cases the true underlying value will not be expected to vary (i.e., data_type = "reps"), or multiple measurements may be taken within an individual and these values are expected to vary (i.e., data_type = "nest").

Replicates

This limit of agreement type is for cases where the underlying values do not vary within subjects. This can be considered cases where replicate measure may be taken. For example, a researcher may want to compare the performance of two ELISA assays where measurements are taken in duplicate/triplicate.

So, you will have to provide the data frame object with the data argument and the names of the columns containing the first (x argument) and second (y argument) must then be provided. An additional column indicating the subject identifier (id) must also be provided.

a2 = agreement_limit(x = "x",
                y = "y",
                id = "id",
                data = reps,
                data_type = "reps",
                agree.level = .8) 

a2
#> MOVER Limits of Agreement (LoA)
#> 80% LoA @ 5% Alpha-Level
#> Data with Replicates
#> 
#>    Bias           Bias CI Lower LoA Upper LoA           LoA CI
#>  0.7152 [-1.5287, 2.9591]    -1.212     2.642 [-4.797, 6.2274]
#> 
#> SD of Differences = 1.5036

Calculative Steps

  1. Compute mean and variance

d‾i=Σj=1nidijni \bar d_i = \Sigma_{j=1}^{n_i} \frac{d_{ij}}{n_i} d‾=Σi=1ndin \bar d = \Sigma^{n}_{i=1} \frac{d_i}{n}

si2=Σj=1ni(dij−d‾i)2ni−1 s_i^2 = \Sigma_{j=1}^{n_i} \frac{(d_{ij} - \bar d_i)^2}{n_i-1}

  1. Compute pooled estimate of within subject error

sdw2=Σi=1n[ni−1N−n⋅si2] s_{dw}^2 = \Sigma_{i=1}^{n} [\frac{n_i-1}{N-n} \cdot s_i^2]

  1. Compute pooled estimate of between subject error

sb2=Σi=1n(d‾i−d‾)2n−1 s^2_b = \Sigma_{i=1}^n \frac{ (\bar d_i - \bar d)^2}{n-1}

  1. Compute the harmonic mean of the replicate size

mh=nΣi=1nmi−1 m_h = \frac{n}{\Sigma_{i=1}^n m_i^{-1}}

  1. Compute SD of the difference

sd2=sb2+(1+mh−1)⋅sdw2 s_d^2 = s^2_b + (1+m_h^{-1}) \cdot s_{dw}^2

  1. Calculate LME

MOVER Method

u=sd2+[sd2⋅(1−n−1χ(1−α,n−1)2)]2+[(1−mh−1)⋅(1−N−nχ(1−α,N−n)2)]2 u = s_d^2 + \sqrt{[s_d^2 \cdot (1 - \frac{n-1}{\chi^2_{(1-\alpha, n-1)}})]^2+[(1-m_h^{-1}) \cdot (1- \frac{N-n}{\chi^2_{(1-\alpha, N-n)}})]^2}

LME=zα⋅sd2n+zβ/22⋅(u−sd2)2 LME = \sqrt{\frac{z_{\alpha} \cdot s_d^2}{n} + z_{\beta/2}^2 \cdot (\sqrt{u}-\sqrt{s^2_d} )^2}

Bland-Altman Method

SLoA2=sd2n+z1−agree22⋅sd2⋅(Sd2n−1+(1−1mxh)2⋅Sxw4Nx−n+(1−1myh)2⋅Syw4Ny−n) S_{LoA}^2 = \frac{s^2_d}{n} + \frac{z_{1-agree}^2}{2 \cdot s_d^2} \cdot (\frac{S_d^2}{n-1} + (1-\frac{1}{m_{xh}})^2 \cdot \frac{S_{xw}^4}{N_x - n} + (1-\frac{1}{m_{yh}})^2 \cdot \frac{S_{yw}^4}{N_y - n})

LME=z1−α⋅SLoA LME = z_{1-\alpha} \cdot S_{LoA}

  1. Calculate LoA

LoAlower=d‾−zβ/2⋅sd LoA_{lower} = \bar d - z_{\beta/2} \cdot s_d

LoAupper=d‾+zβ/2⋅sd LoA_{upper} = \bar d + z_{\beta/2} \cdot s_d

  1. Calculate LoA CI

$$ Lower \space CI = LoA_{lower} - LME $$

$$ Upper \space CI = LoA_{upper} + LME $$

Nested

This is for cases where the underlying values may vary within subjects. This can be considered cases where there are distinct pairs of data wherein data is collected in different times/conditions within each subject. An example would be measuring blood pressure on two different devices on many people at different time points/days. The method utilized in agreement_limit is similar to, but not the exact same as those described by Zou (2011). However, the results should be approximately the same as agree_nest and should provide estimates that are very close to those described by Zou (2011).

a3 = agreement_limit(x = "x",
                y = "y",
                id = "id",
                data = reps,
                data_type = "nest",
                loa_calc = "mover",
                agree.level = .95)
#> Cannot use mode = "satterthwaite" because *lmerTest* package is not installed
a3
#> MOVER Limits of Agreement (LoA)
#> 95% LoA @ 5% Alpha-Level
#> Nested Data
#> 
#>    Bias           Bias CI Lower LoA Upper LoA            LoA CI
#>  0.7046 [-1.5512, 2.9604]    -2.153     3.562 [-7.4979, 8.9071]
#> 
#> SD of Differences = 1.4581

Calculation Steps

  1. Model

A linear mixed model (detailed below) is fit to estimate the bias (mean difference) and variance components (within and between subject variance).

differencei∼N(αj[i],σ2)αj∼N(μαj,σαj2), for subject j = 1,…,J \begin{aligned} \operatorname{difference}_{i} &\sim N \left(\alpha_{j[i]}, \sigma^2 \right) \\ \alpha_{j} &\sim N \left(\mu_{\alpha_{j}}, \sigma^2_{\alpha_{j}} \right) \text{, for subject j = 1,} \dots \text{,J} \end{aligned} 2. Extract Components

The two variance components, (sb2s_b^2 and sw2s_w^2 for σ2\sigma^2 and σαj2\sigma_{\alpha_j}^2), are estimated from the model. The sum of both (stotal2s_{total}^2) is the total variance, and grand intercept represents the bias (mean difference, d‾\bar d).

The harmonic mean is also calculated.

mh=nΣi=1nmi−1 m_h = \frac{n}{\Sigma_{i=1}^n m_i^{-1}}

  1. Compute LME

MOVER Method

u1=(sb2⋅((n−1)/(χα,n−12)−1))2 u_1 = (s_b^2 \cdot ((n-1)/(\chi^2_{\alpha,n-1})-1))^2

u2=((1−1/mh)⋅sw2⋅((N−n)/(χα,N−n2−1))2 u_2 = ((1-1/m_h) \cdot s_w^2 \cdot ((N-n)/( \chi^2_{\alpha,N-n} -1))^2

u=stotal2+u1+u2 u = s_{total}^2 + \sqrt{u_1 + u_2}

LME=zα2⋅sd2n+zβ/22⋅(u−sd2)2 LME = \sqrt{\frac{z^2_{\alpha} \cdot s_d^2}{n} + z^2_{\beta/2} \cdot(\sqrt{u} - \sqrt{s^2_d})^2}

Bland-Altman Method

SLoA=sb2n+zagree2/(2⋅stotal2)⋅((sb2)2/(n−1)+(1−1/mh)2⋅(sw2)2/(N−n)) S_{LoA} = \frac{s_b^2}{n} + z_{agree}^2 / (2 \cdot s_{total}^2) \cdot ((s_b^2)^2/(n-1) + (1 - 1/m_h)^2 \cdot (s_{w}^2)^2/(N-n)) LME=z1−α⋅SLoA LME = z_{1-\alpha} \cdot S_{LoA}

  1. Calculate LoA

LoAlower=d‾−zβ/2⋅sd LoA_{lower} = \bar d - z_{\beta/2} \cdot s_d

LoAupper=d‾+zβ/2⋅sd LoA_{upper} = \bar d + z_{\beta/2} \cdot s_d

  1. Calculate LoA CI

$$ Lower \space CI = LoA_{lower} - LME $$

$$ Upper \space CI = LoA_{upper} + LME $$

How to Test a Hypothesis

Unlike the “test” functions, agreement_limits and tolerance_limits do not test a hypothesis agreement, but only estimate the limits. It is up to the user to determine if the limits are within a maximal allowable difference. However, the results a maximal allowable difference can be visualized against the tolerance/agreement limits using the delta argument for the plot method.

res1 = tolerance_limit(
  data = temps,
  x = "trec_pre", # First measure
  y = "teso_pre", # Second measure
  id = "id", # Subject ID
  condition = "tod", # Identify condition that may affect differences
  cor_type = "sym" # Set correlation structure as Compound Symmetry
)
plot(res1, delta = .25) # Set maximal allowable difference to .25 units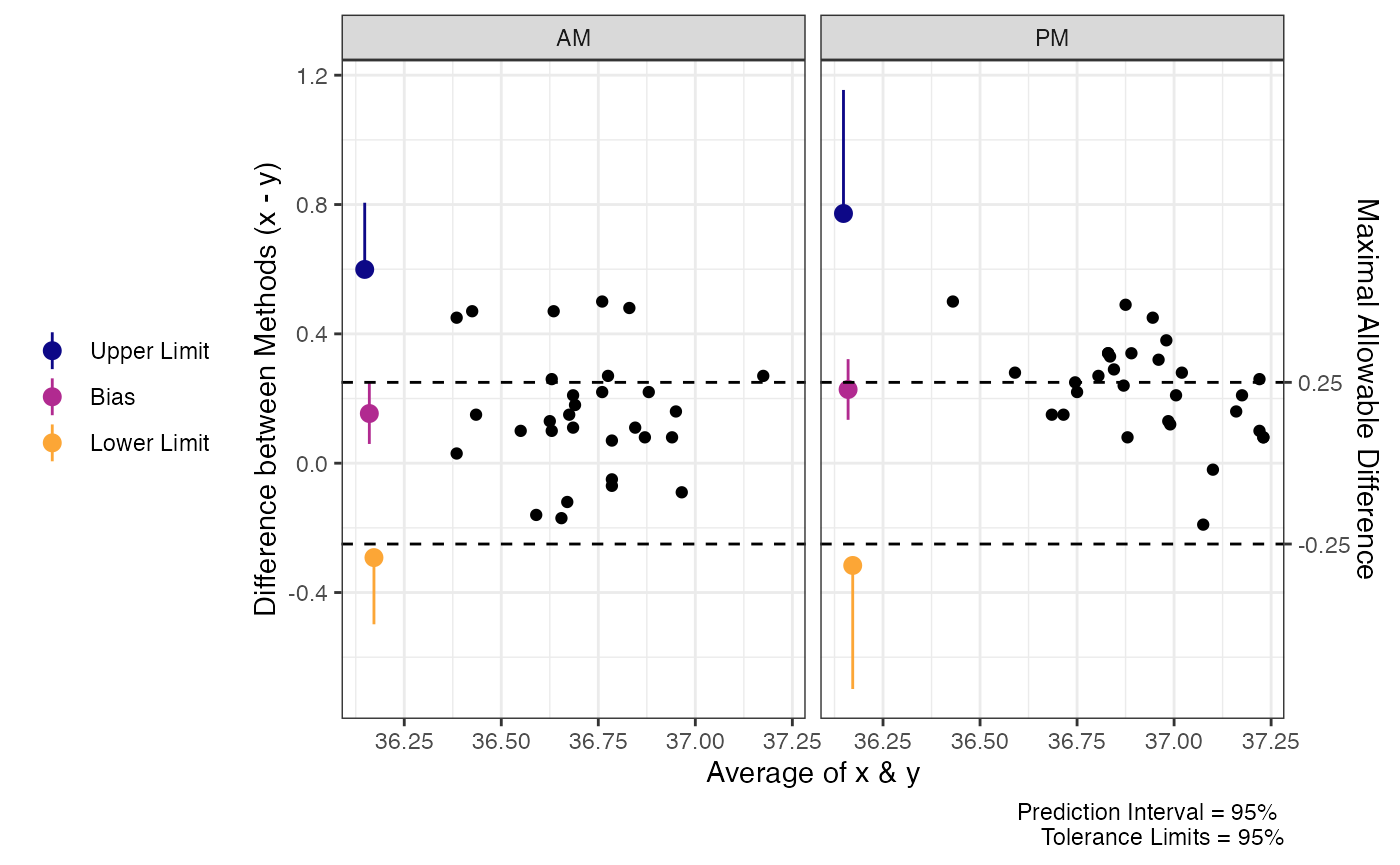

Checking Assumptions

The assumptions of normality, heteroscedasticity, and proportional bias can all be checked using the check method for either agreement or tolerance limits.

The function will provide 3 plots: Q-Q normality plot, standardized residuals plot, and proportional bias plot.

All 3 plots will have a statistical test in the bottom right corner2. The Shapiro-Wilk test is included for the normality plot, the Bagan-Preusch test for heterogeneity, and the test for linear slope on the residuals plot. Please note that there is no formal test of proportional bias for the tolerance limits, but a plot is still included for visual checks.

An Example 

test_agree = agreement_limit(x = "x",
                             y = "y",
                             data = reps)

check(test_agree)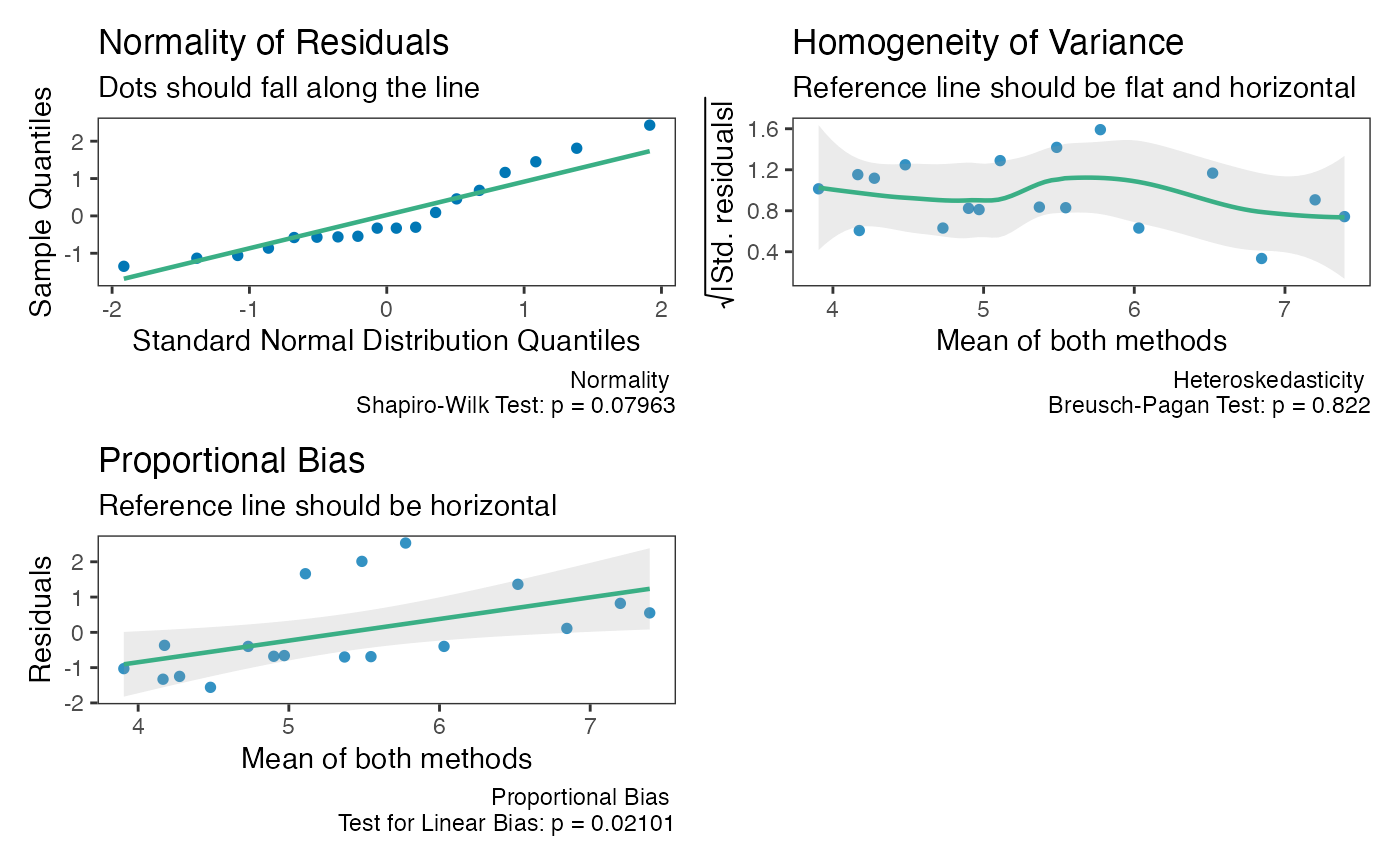


test_tol = tolerance_limit(x = "x",
                           y = "y",
                           data = reps)

check(test_tol)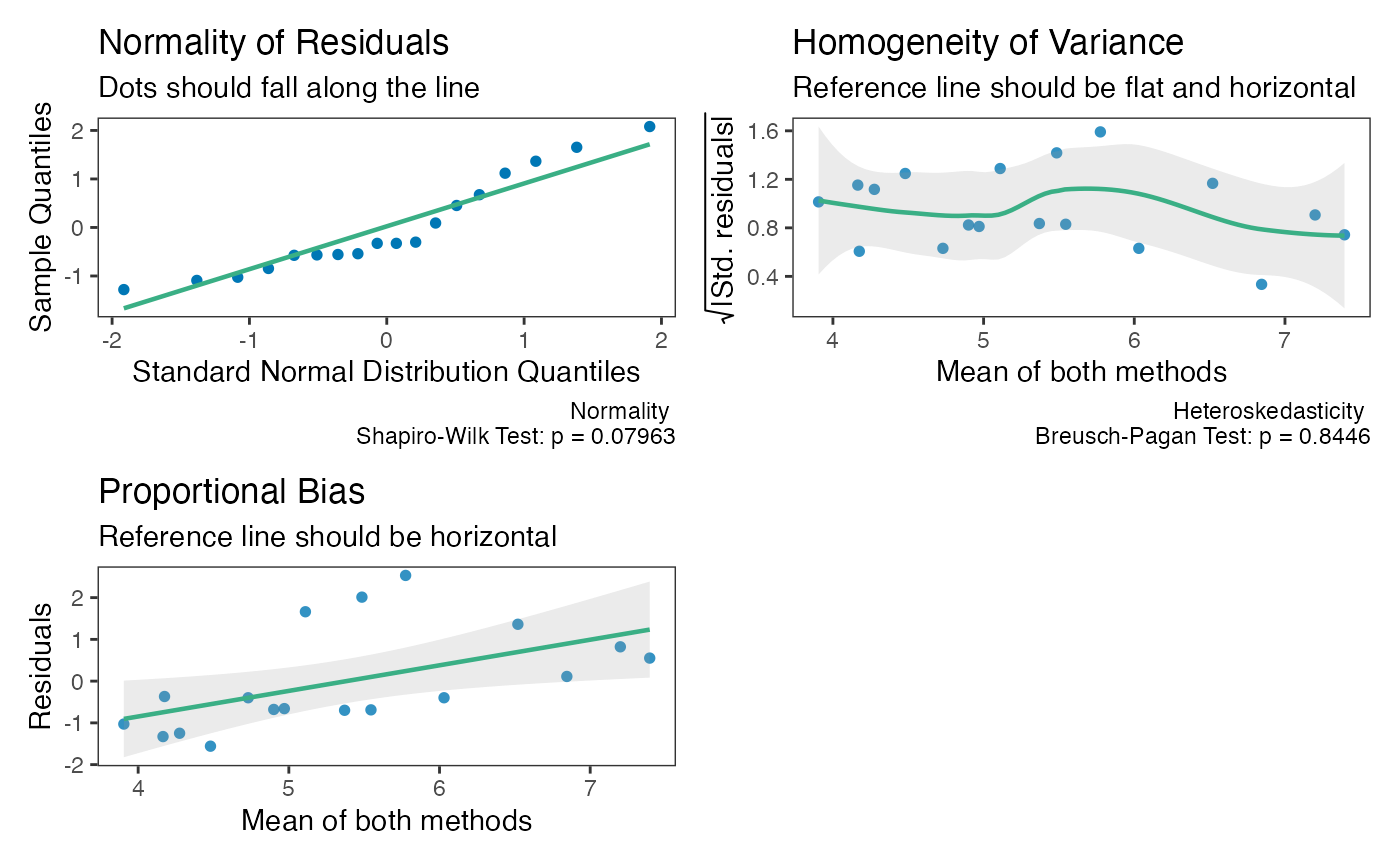

Proportional Bias

As the check plots for a1 show, proportional bias can sometimes occur. In these cases Bland and Altman (1999) recommended adjusting the bias and LoA for the proportional bias. This is simply done by include a slope for the average of both measurements (i.e, using an intercept + slope model rather than intercept only model).

For either agreement_limit or tolerance_limit functions, this can be accomplished with the prop_bias argument. When this is set to TRUE, then the proportional bias adjusted model is utilized. Plots and checks of the data should always be inspected.


test_tol = tolerance_limit(x = "x",
                           y = "y",
                           data = reps,
                           prop_bias = TRUE)
print(test_tol)
#> Agreement between Measures (Difference: x-y)
#> 95% Prediction Interval with 95% Tolerance Limits
#> 
#>  Average of Both Methods    Bias           Bias CI Prediction Interval
#>                    3.905 -0.4670 [-1.3842, 0.4502]   [-2.8876, 1.9537]
#>                    5.240  0.3513 [-0.1816, 0.8842]    [-1.9513, 2.654]
#>                    7.395  1.6723  [0.5218, 2.8228]    [-0.846, 4.1906]
#>   Tolerance Limits
#>  [-3.6396, 2.7057]
#>  [-2.6667, 3.3694]
#>  [-1.6284, 4.9729]

# See effect of proportional bias on limits
plot(test_tol)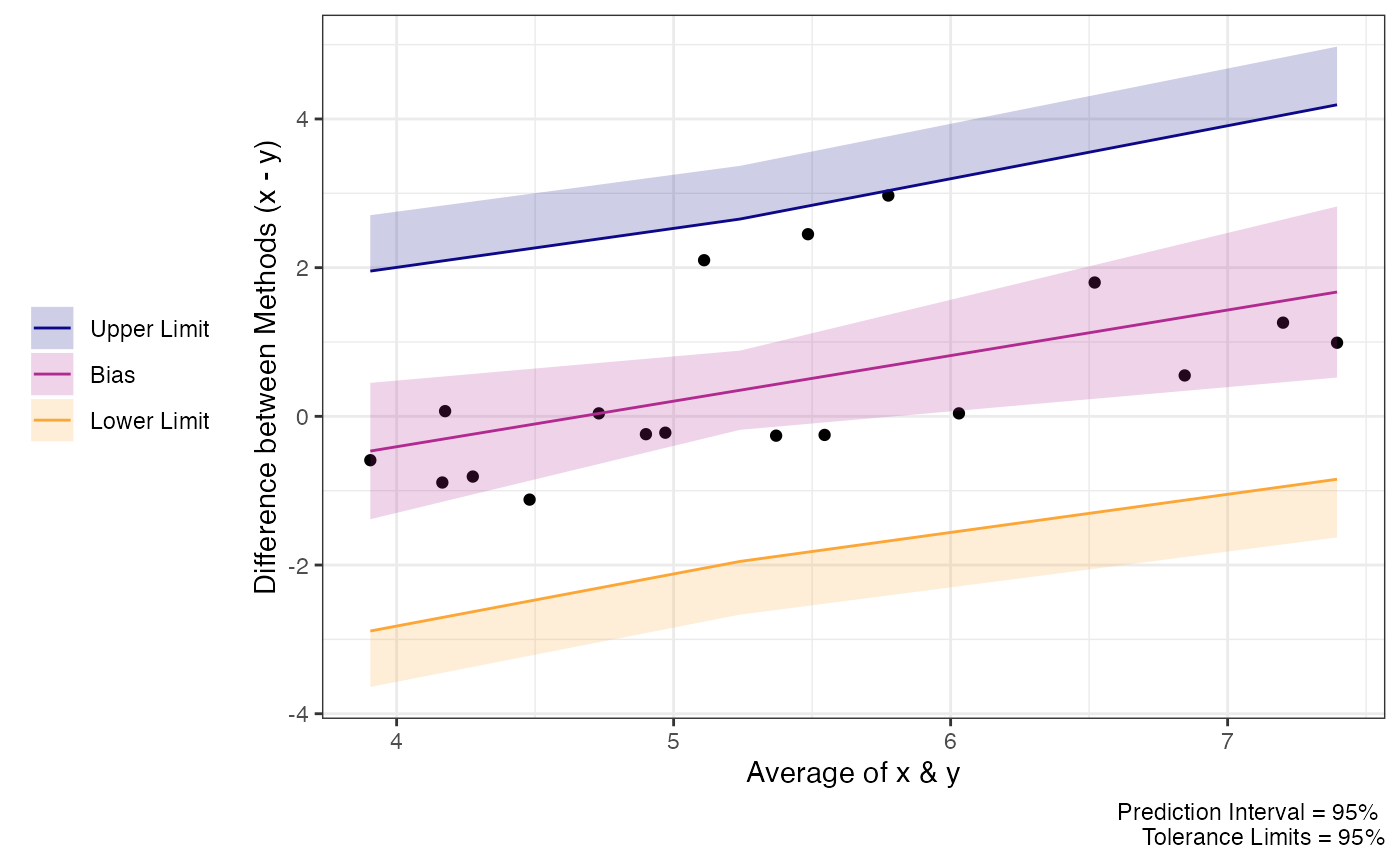


# Confirm its effects in proportional bias check plot (should be horizontal now)
check(test_tol)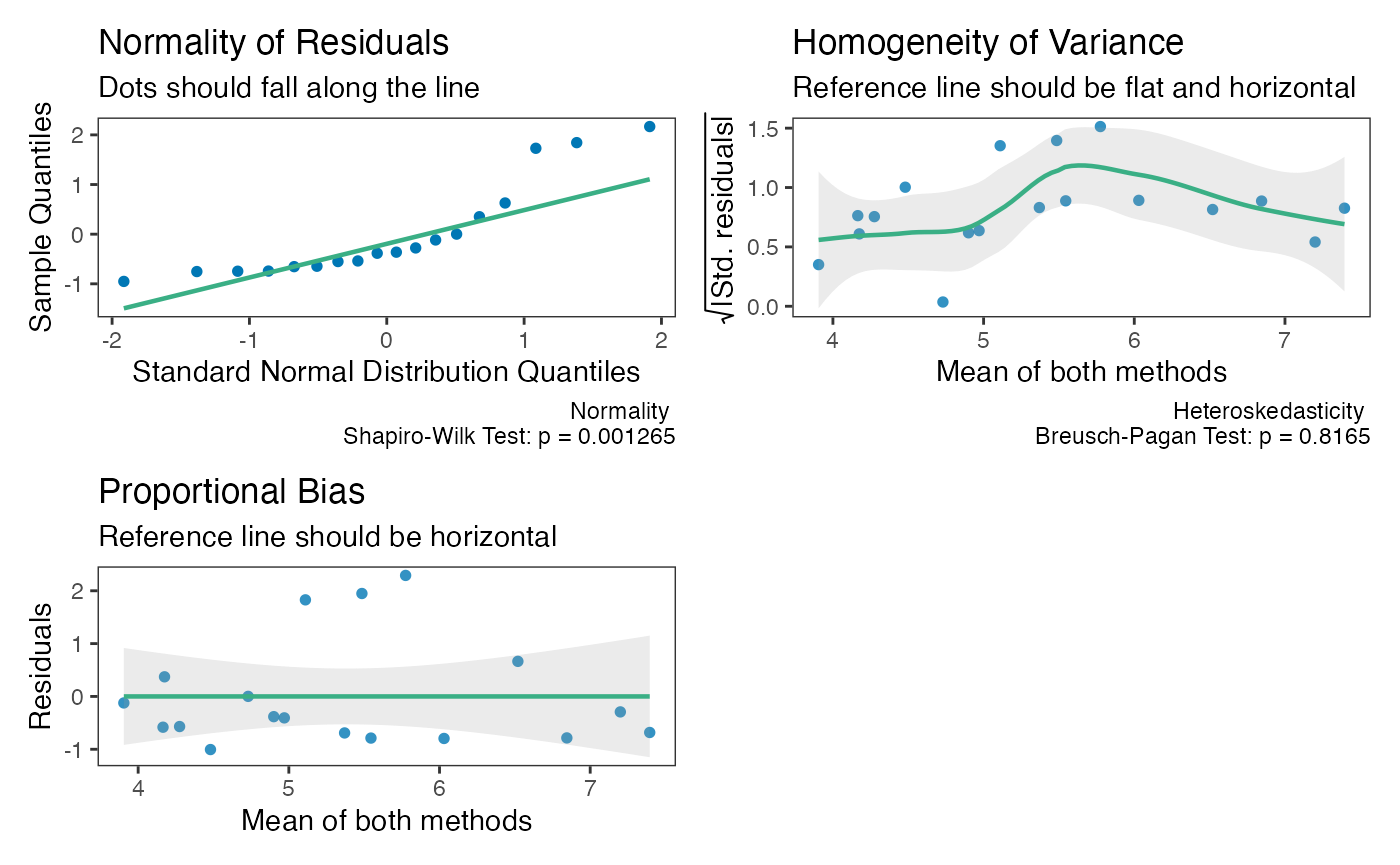

Log transformation

Sometimes a log transformation may be a useful way of “normalizing” the data. Most often this is done when the error is proportional to the mean. The interpretation is also easy because the differences (when back transformed) can be interpreted as ratios. The log transformation (natural base) can be accomplished with the log_tf argument.

tolerance_limit(
  data = temps,
  log_tf = TRUE, # natural log transformation of responses
  x = "trec_pre", # First measure
  y = "teso_pre", # Second measure
  id = "id", # Subject ID
  condition = "tod", # Identify condition that may affect differences
  cor_type = "sym" # Set correlation structure as Compound Symmetry
)
#> Agreement between Measures (Ratio: x/y)
#> 95% Prediction Interval with 95% Tolerance Limits
#> 
#>  Condition  Bias          Bias CI Prediction Interval Tolerance Limits
#>         AM 1.004 [1.0016, 1.0068]    [0.9921, 1.0165] [0.9865, 1.0222]
#>         PM 1.006 [1.0036, 1.0088]    [0.9913, 1.0213]  [0.981, 1.0321]

If you prefer to interpret the differences as a percentage difference, you can do this by setting the log_tf_display argument to “sympercent”. This stands for the “symmetric percentage difference” which is the log transformed differences between the measures, s%=(log(x)−log(y))⋅100%=log(x/y)⋅100%s\% = (log(x)-log(y) ) \cdot 100\% = log(x/y) \cdot 100\%, and can be interpreted as a percentage difference between the two paired measures.

tolerance_limit(
  data = temps,
  log_tf = TRUE, # natural log transformation of responses
  log_tf_display = "sympercent", # display results as sympercent
  x = "trec_pre", # First measure
  y = "teso_pre", # Second measure
  id = "id", # Subject ID
  condition = "tod", # Identify condition that may affect differences
  cor_type = "sym" # Set correlation structure as Compound Symmetry
)
#> Sympercent Difference between Methods (s%)
#> 95% Prediction Interval with 95% Tolerance Limits
#> 
#>  Condition   Bias          Bias CI Prediction Interval  Tolerance Limits
#>         AM 0.4188  [0.1616, 0.676]   [-0.7958, 1.6334] [-1.3558, 2.1934]
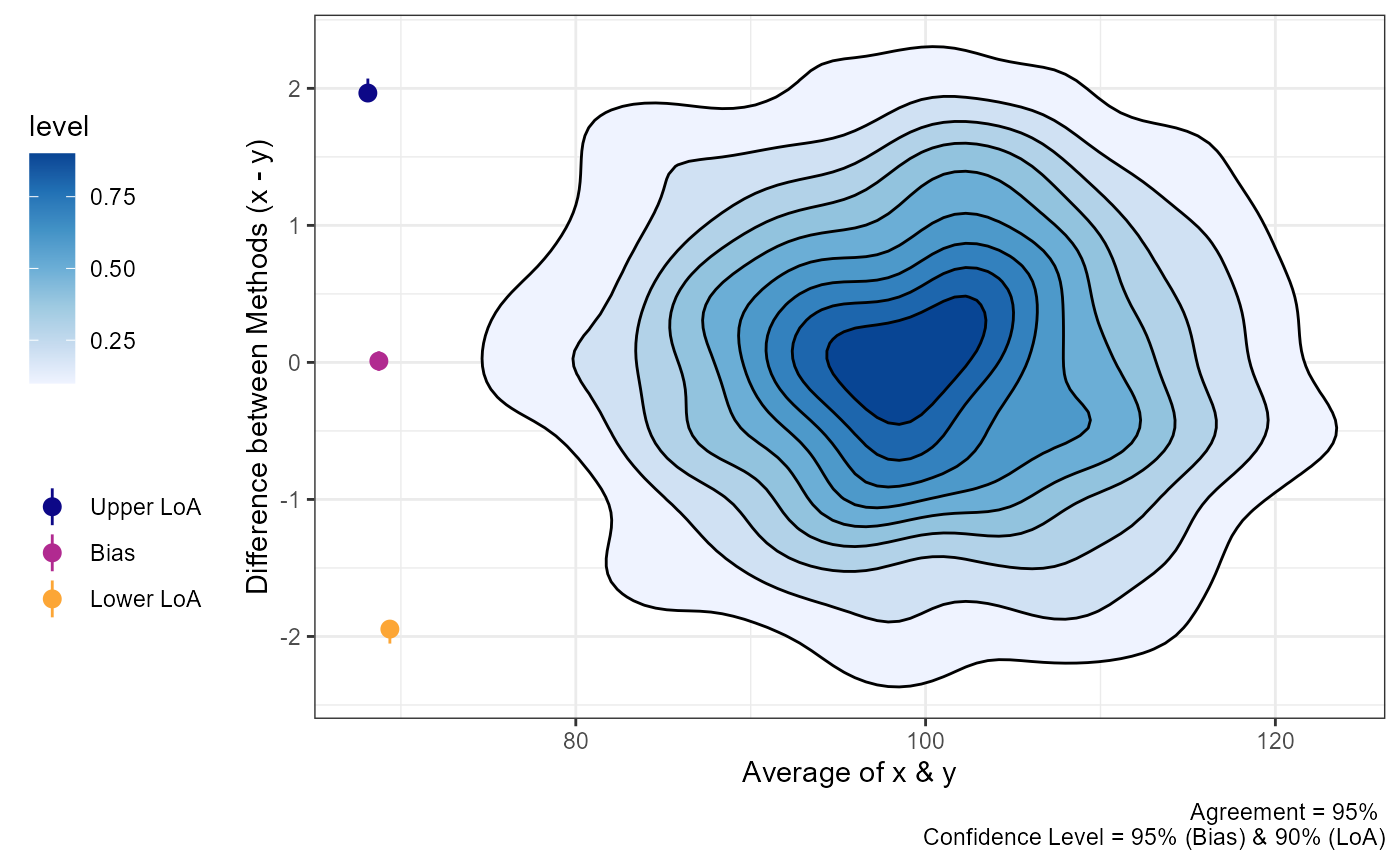
#>         PM 0.6184 [0.3622, 0.8746]   [-0.8703, 2.1072] [-1.9189, 3.1558]

Visualizing “Big” Data

Sometimes there may be a lot of data and individual points of data on mean difference visualization may be less than ideal. In order to change the plots from showing the individual data points we can modify the geom argument.

set.seed(81346)
x = rnorm(750, 100, 10)
diff = rnorm(750, 0, 1)
y = x + diff

df = data.frame(x = x,
                y = y)

a1 = agreement_limit(data = df,
                     x = "x",
                     y = "y",
                     agree.level = .95)

plot(a1,
     geom = "geom_point")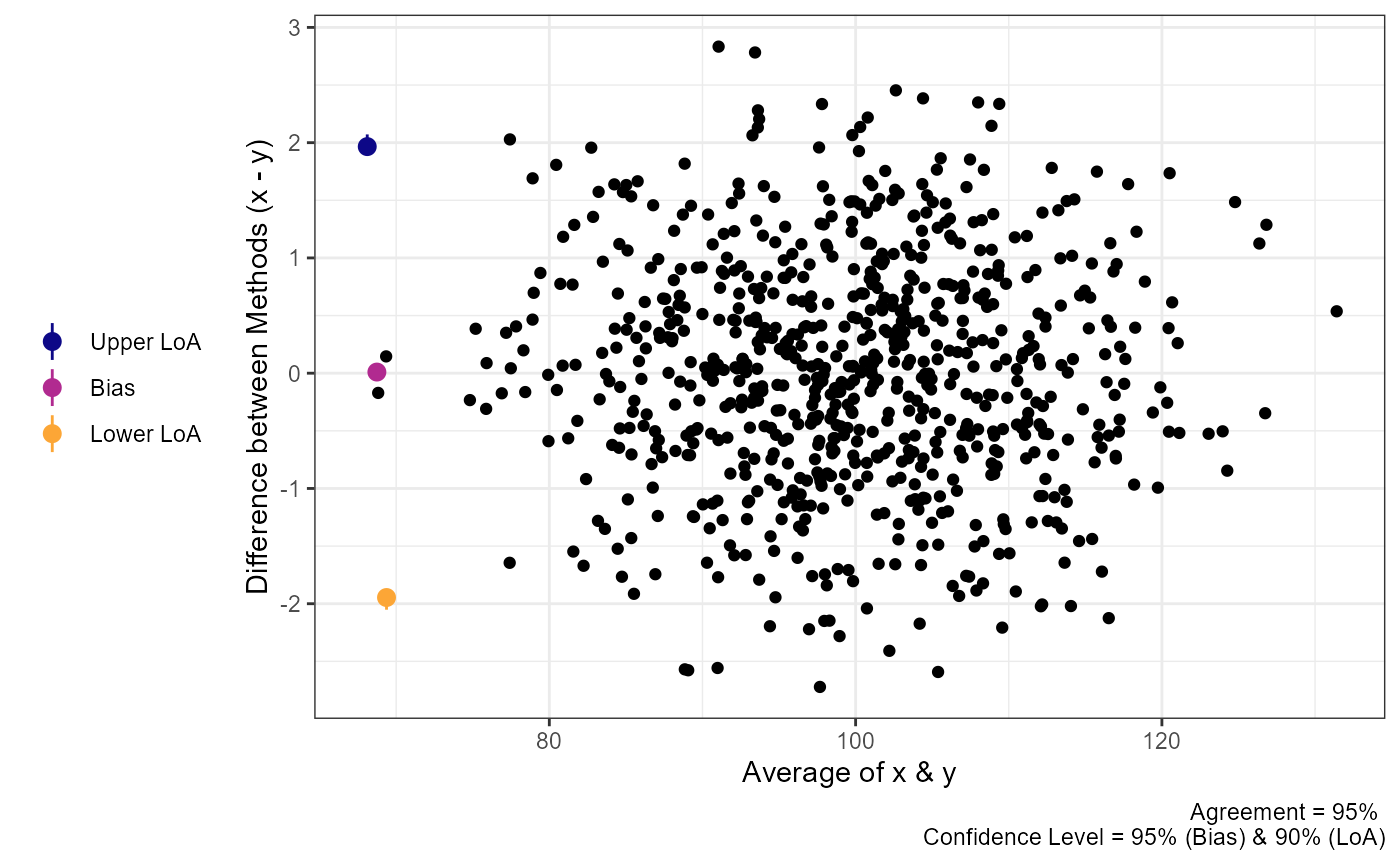


plot(a1,
     geom = "geom_bin2d")


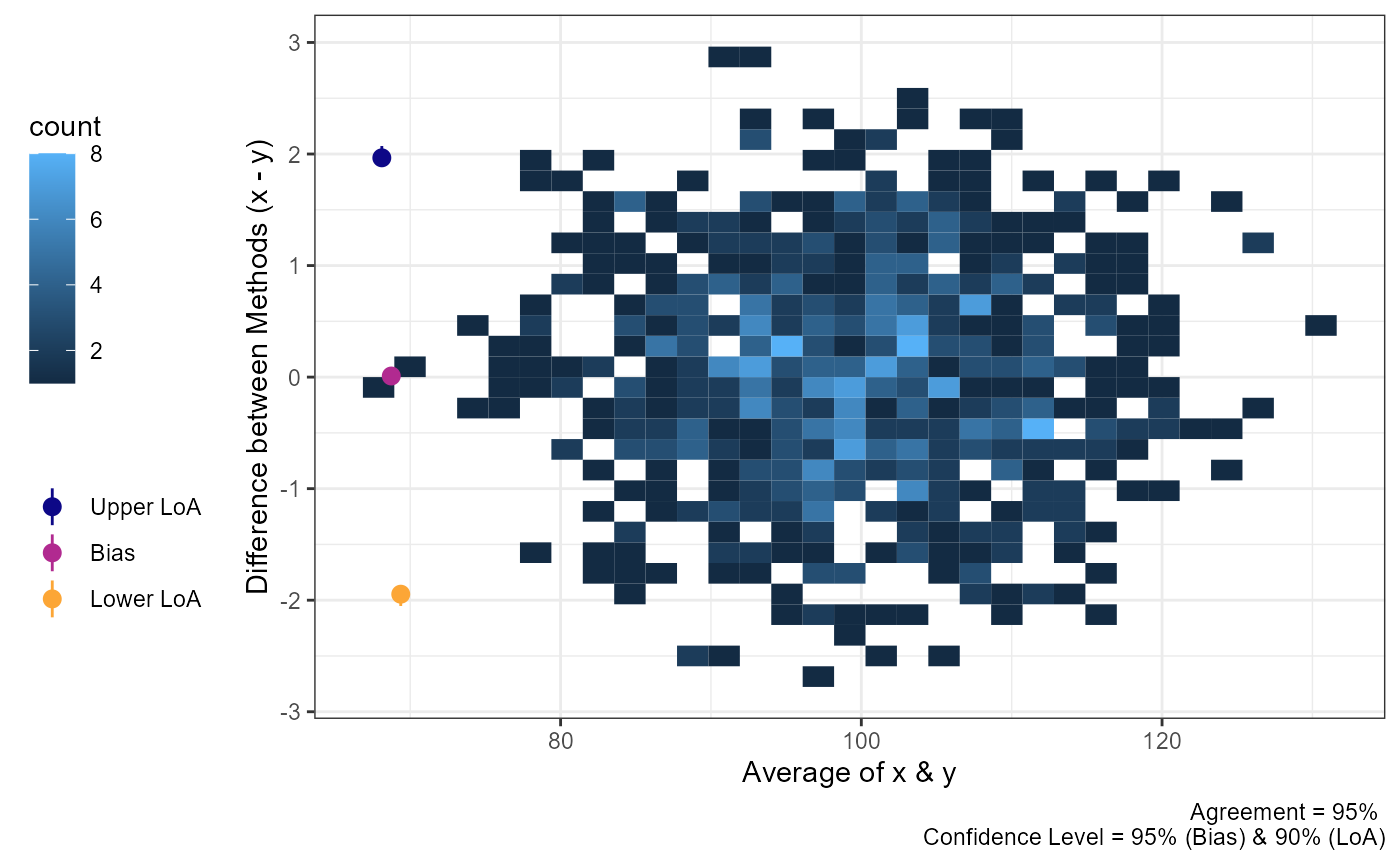
plot(a1,
     geom = "geom_density_2d")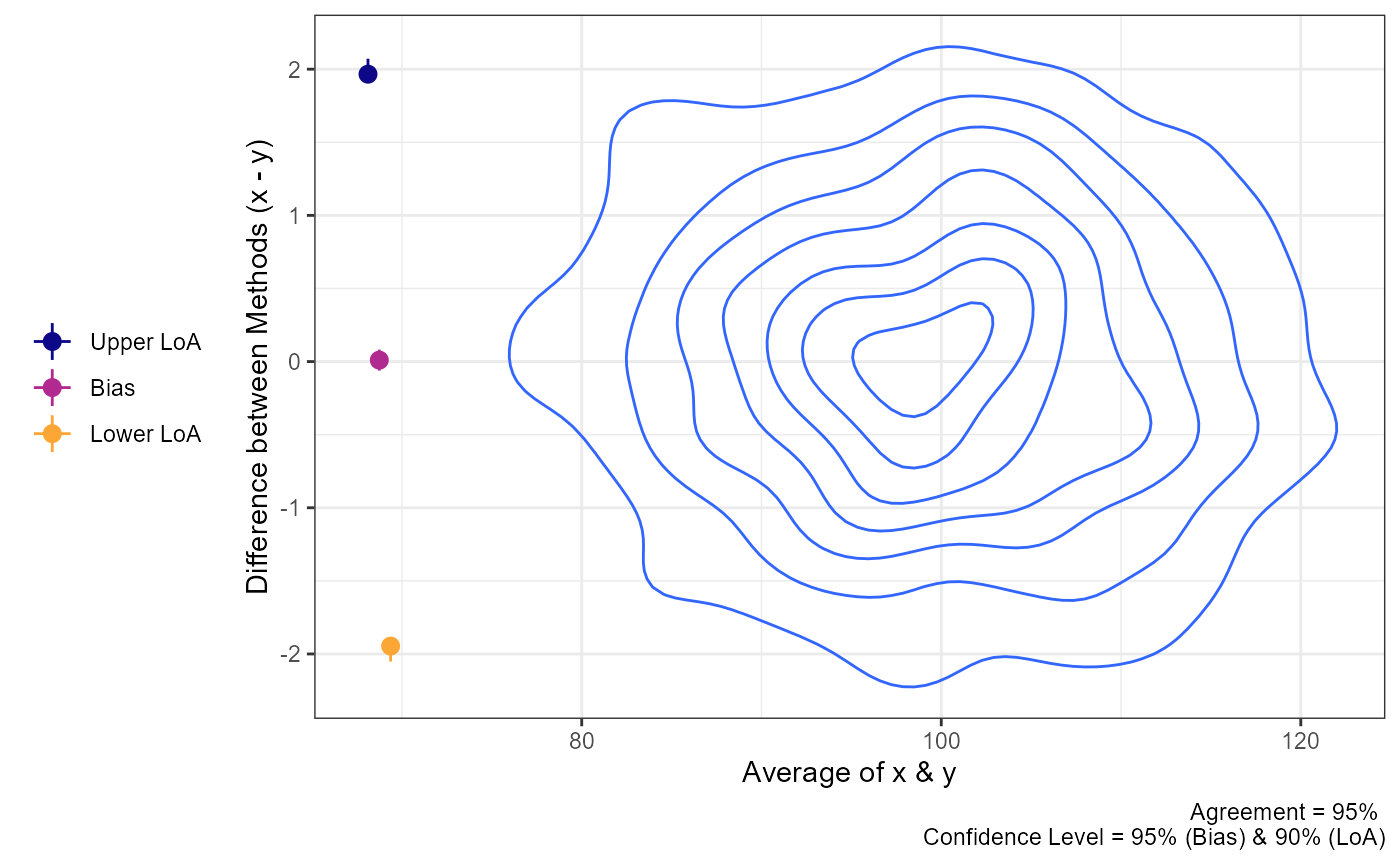


plot(a1,
     geom = "geom_density_2d_filled")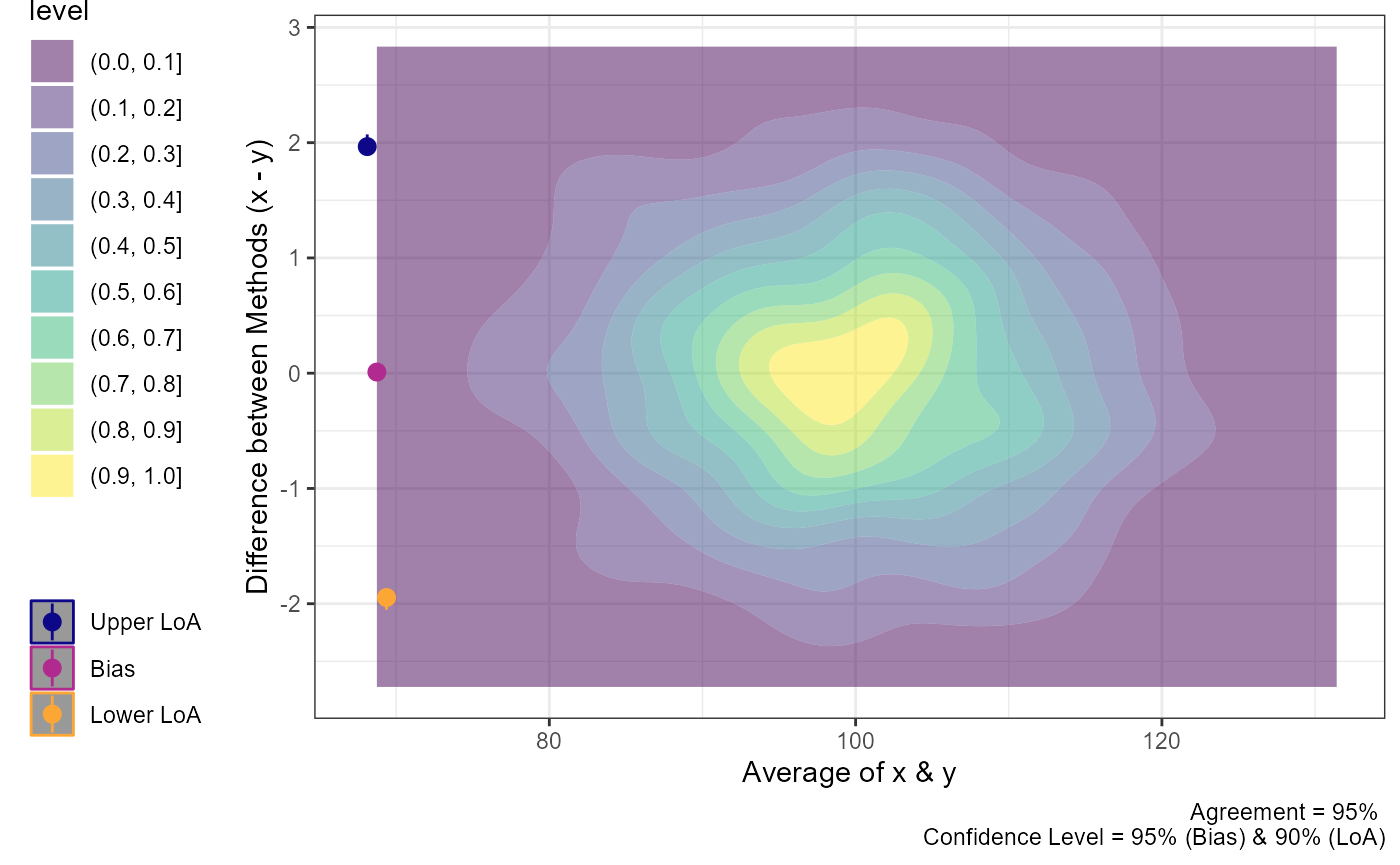


plot(a1,
     geom = "stat_density_2d")

References

Bland, J Martin, and Douglas G Altman. 1986. “Statistical Methods for Assessing Agreement Between Two Methods of Clinical Measurement.” The Lancet 327 (8476): 307–10. https://doi.org/10.1016/s0140-6736(86)90837-8.
———. 1999. “Measuring Agreement in Method Comparison Studies.” Statistical Methods in Medical Research 8 (2): 135–60. https://doi.org/10.1177/096228029900800204.
Donner, Allan, and GY Zou. 2012. “Closed-Form Confidence Intervals for Functions of the Normal Mean and Standard Deviation.” Statistical Methods in Medical Research 21 (4): 347–59.
Francq, Bernard G, Marion Berger, and Charles Boachie. 2020. “To Tolerate or to Agree: A Tutorial on Tolerance Intervals in Method Comparison Studies with BivRegBLS r Package.” Statistics in Medicine 39 (28): 4334–49.
Kuznetsova, Alexandra, Per B Brockhoff, and Rune HB Christensen. 2017. “lmerTest Package: Tests in Linear Mixed Effects Models.” Journal of Statistical Software 82: 1–26.
Satterthwaite, Franklin E. 1946. “An Approximate Distribution of Estimates of Variance Components.” Biometrics Bulletin 2 (6): 110–14.
Young, Derek S. 2010. “Tolerance: An r Package for Estimating Tolerance Intervals.” Journal of Statistical Software 36: 1–39.
Zou, GY. 2011. “Confidence Interval Estimation for the Blandaltman Limits of Agreement with Multiple Observations Per Individual.” Statistical Methods in Medical Research 22 (6): 630–42. https://doi.org/10.1177/0962280211402548.

  1. Pinheiro, J.C., and Bates, D.M. (2000) “Mixed-Effects Models in S and S-PLUS”, Springer, pp. 100, 461.↩︎

  2. No test is included for proportional bias for tolerance_limit results at this time.↩︎