TOST Independent Samples T-Test — dataTOSTtwo • TOSTER

TOST Independent Samples T-Test for jamovi. This function is not meant to be utilized in R. See t_TOST function.

dataTOSTtwo(
  data,
  deps,
  group,
  var_equal = FALSE,
  hypothesis = "EQU",
  low_eqbound = -0.5,
  high_eqbound = 0.5,
  eqbound_type = "raw",
  alpha = 0.05,
  desc = FALSE,
  plots = FALSE,
  descplots = FALSE,
  low_eqbound_d = -999999999,
  high_eqbound_d = -999999999,
  smd_type = "g"
)

Arguments

data: the data as a data frame
deps: a vector of strings naming dependent variables in data
group: a string naming the grouping variable in data; must have two levels
var_equal: TRUE or FALSE (default), assume equal variances
hypothesis: 'EQU' for equivalence (default), or 'MET' for minimal effects test, the alternative hypothesis.
low_eqbound: a number (default: -0.5) the lower equivalence/MET bounds
high_eqbound: a number (default: 0.5) the upper equivalence/MET bounds
eqbound_type: 'SMD' (default) or 'raw'; whether the bounds are specified in Cohen's d or raw units respectively
alpha: alpha level (default = 0.05)
desc: TRUE or FALSE (default), provide descriptive statistics
plots: TRUE or FALSE (default), provide effect size plots
descplots: TRUE or FALSE (default), provide plots
low_eqbound_d: deprecated
high_eqbound_d: deprecated
smd_type: 'd' (default) or 'g'; whether the calculated effect size is biased (d) or bias-corrected (g).

Value

A results object containing:

`results$text`					a html
`results$tost`					a table
`results$eqb`					a table
`results$effsize`					a table
`results$desc`					a table
`results$plots`					an array of images
`results$descplots`					an array of images

Tables can be converted to data frames with asDF or as.data.frame. For example:

results$tost$asDF

as.data.frame(results$tost)

References

Berger, R. L., & Hsu, J. C. (1996). Bioequivalence Trials, Intersection-Union Tests and Equivalence Confidence Sets. Statistical Science, 11(4), 283-302.

Gruman, J. A., Cribbie, R. A., & Arpin-Cribbie, C. A. (2007). The effects of heteroscedasticity on tests of equivalence. Journal of Modern Applied Statistical Methods, 6(1), 133-140, formula for Welch's t-test on page 135

Examples

library(TOSTER)

## Load iris dataset, remove one of the three groups so two are left

data<-iris[which(iris$Species!="versicolor"),]

## TOST procedure on the raw data

dataTOSTtwo(data, deps="Sepal.Width", group="Species", var_equal = TRUE, low_eqbound = -0.5,
            high_eqbound = 0.5, alpha = 0.05, desc = TRUE, plots = TRUE)
#> 
#>  TOST INDEPENDENT SAMPLES T-TEST
#> 
#>  Hypothesis Tested: Equivalence
#> 
#>  Null Hypothesis: -0.5 &ge; (Mean1 - Mean2) or (Mean1 - Mean2) &ge; 0.5
#>  Alternative: -0.5 < (Mean1 - Mean2) < 0.5
#>  &#9989 NHST: reject null significance hypothesis that the effect is
#>  equal to zero
#>  &#10060 TOST: don't reject null equivalence hypothesis
#> 
#>  Note: SMD confidence intervals are an approximation. See our <a
#>  href="https://aaroncaldwell.us/TOSTERpkg/articles/SMD_calcs.html">documentation.
#> 
#>  TOST Results                                                          
#>  ───────────────────────────────────────────────────────────────────── 
#>                                 t             df          p            
#>  ───────────────────────────────────────────────────────────────────── 
#>    Sepal.Width    t-test          6.450349    98.00000    < .0000001   
#>                   TOST Lower      13.55426    98.00000    < .0000001   
#>                   TOST Upper    -0.6535596    98.00000     0.2574631   
#>  ───────────────────────────────────────────────────────────────────── 
#> 
#> 
#>  Equivalence Bounds                                       
#>  ──────────────────────────────────────────────────────── 
#>                                 Low           High        
#>  ──────────────────────────────────────────────────────── 
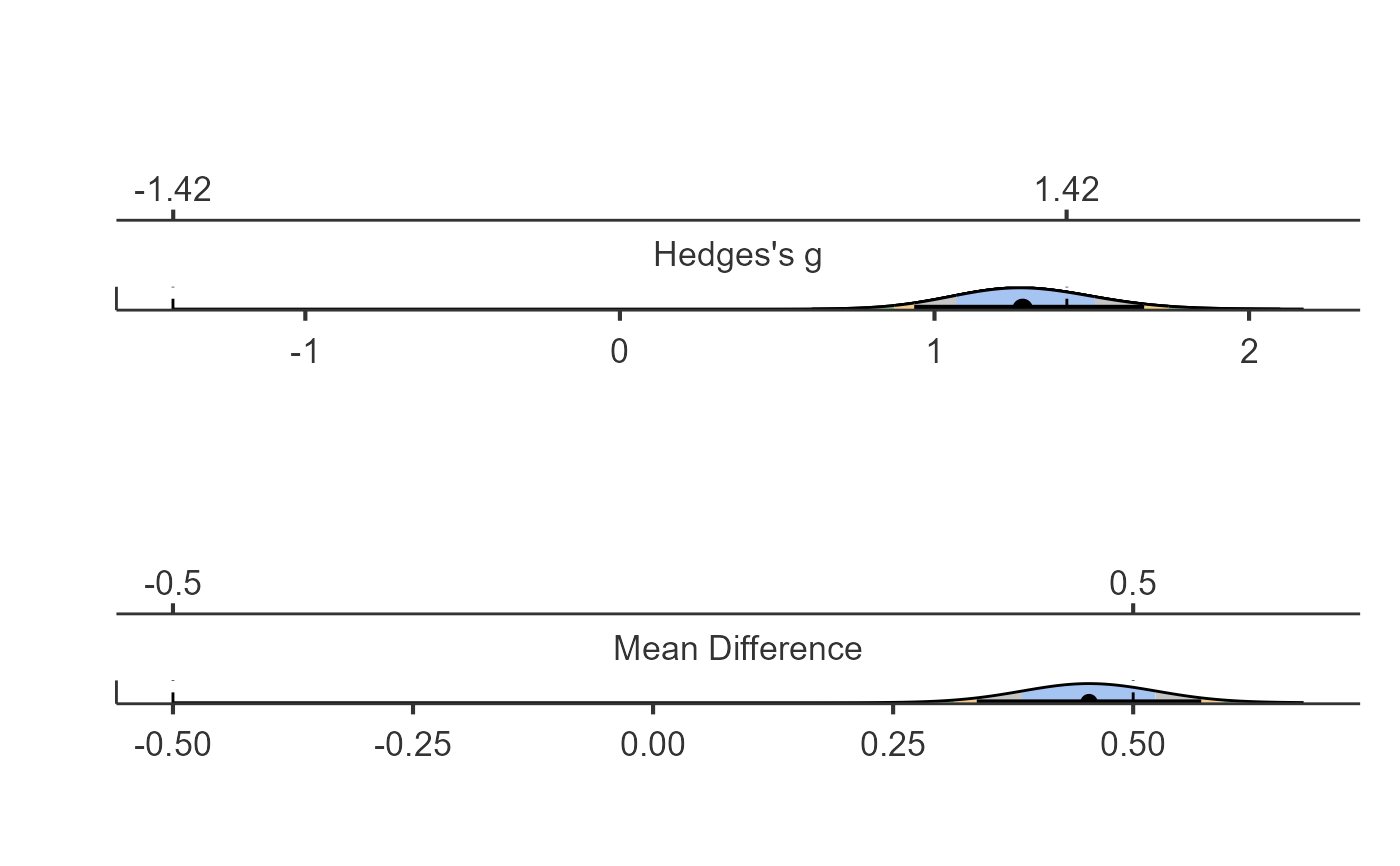
#>    Sepal.Width    Hedges's g     -1.420782     1.420782   
#>                   Raw           -0.5000000    0.5000000   
#>  ──────────────────────────────────────────────────────── 
#> 
#> 
#>  Effect Sizes                                                         
#>  ──────────────────────────────────────────────────────────────────── 
#>                                 Estimate     Lower        Upper       
#>  ──────────────────────────────────────────────────────────────────── 
#>    Sepal.Width    Hedges's g     1.280167    0.9356088     1.666477   
#>                   Raw           0.4540000    0.3371241    0.5708759   
#>  ──────────────────────────────────────────────────────────────────── 
#>    Note. Denominator set to the pooled SD
#> 
#> 
#>  Descriptives                                                         
#>  ──────────────────────────────────────────────────────────────────── 
#>               N     Mean        Median      SD           SE           
#>  ──────────────────────────────────────────────────────────────────── 
#>    Group 1    50    3.428000    3.400000    0.3790644    0.05360780   
#>    Group 2    50    2.974000    3.000000    0.3224966    0.04560791   
#>  ──────────────────────────────────────────────────────────────────── 
#>