Updated on: 2024-01-18

Introduction

There have been a number of criticisms of “magnitude-based inferences” (Batterham and Hopkins 2006) which is a unique approach to statistics in the sport and exercise science community. As an author of the mbir package (Peterson and Caldwell 2019), I have been watching this all develop closely. What is clear from the criticisms is that MBI has some fatal flaws directly related to the sample size estimations and the interpretations of the probabilities that the MBI spreadsheets provide (Lohse et al. 2020; K. L. Sainani et al. 2019; K. Sainani 2018). One of my motivations for helping make mbir was to ensure there was version control of this technique, and that any changes to MBI would be well-documented. Now is the time for changes, and in this short post I will document how apply MBI in a frequentist hypothesis testing framework. The statistical reasoning behind this approach has been outlined in detail by Aisbett, Lakens, and Sainani (2020). I was lucky enough to provide feedback on an earlier version of this manuscript and it inspired me to write this blog post. Changes to mbir will hopefully come soon once Kyle and I agree upon the appropriate path forward for the package (we may add Bayesian options as well). In this document, I will detail how to implement the approach of Aisbett, Lakens, and Sainani (2020) in R and SAS. My hope is that with these details sport and exercise scientists can do three things: 1) go beyond relying entirely on ‘significance’, 2) avoid the pitfalls of the “old” MBI, and 3) apply analyses that have been well-documented in the statistics literature.

Note of caution

This blog post implicitly assumes researchers are interested in testing hypotheses. This is often not the case for many sport scientists. Researchers may simply want to estimate the magnitude an effect, or may be using inferential statistics as descriptions of the data (Chow and Greenland 2019; Greenland and Chow 2019; Amrhein, Trafimow, and Greenland 2019). Personally, I have no problem with these approaches and would highly recommend the concurve R package as a visualization tool if that is your intention (Rafi and Vigotsky 2020).

The Basic Concepts

For those of you that have not read Aisbett, Lakens, and Sainani (2020), I will quickly detail what their approach entails. The primary point of their paper is that MBI can be described as combination of two one-sided tests (TOST) for equivalence testing and minimal effects tests (MET). The difference between this approach and the old MBI approach is that now researchers will have to establish an a priori alpha-level, a smallest effect size of interest (SESOI), and justify their sample size on the basis of statistical power. In this format, we must explicitly test hypotheses and remove references to effects being “likely or very likely” or “unclear”, but rather state whether the data is “compatible, inconclusive, or ambiguous” depending on the result (See Table 6 of Aisbett, Lakens, & Sainani 2020). There are other more specific recommendations (such as the removal of the odds ratio calculations), and I highly recommend everyone read Aisbett, Lakens, and Sainani (2020) for more details.

Terminology

Equivalence Testing is a procedure designed to test whether an effect is contained within an equivalence bound. Many people may be familiar with equivalence testing from using TOST (Daniël Lakens, Scheel, and Isager 2018a). This establishes a null hypothesis that the effect is greater, or less, than the equivalence bound, and the alternative would be that the effect is within the equivalence bound.

Minimal Effects Testing (MET) is a test to determine whether an effect is large enough to be considered meaningful. In contrast to equivalence testing, a null hypothesis in MET is that the effect is less than an minimal effects bound and the alternative would be that the effect is greater than the bound.

Non-Inferiority Testing is a test of whether is not worse than a inferiority margin. For example, this is commonly used in bio-pharmaceutical trials where a new, typically cheaper, drug is being introduced and the study is completed simply to show it does not perform worse than the existing option(s).

To visualize what these new terms mean, take a look at Figure 1 adapted from Daniël Lakens, Scheel, and Isager (2018b). A Bayesian interpreation of this can also be found in a recent manuscript from Ravenzwaaij et al. (2019). In essence, we have 2 sets of tests that MBI is using “under-the-hood” when calculating the percentages for each effect. For mechanistic MBI, the “decisions” are made using a combination of TOST & MET. For clinical MBI, the “decisions” are made with a combination of MET and a non-inferiority test with, most likely, differing alphas. Now, under the new approach, you are explicitly stated your hypotheses and testing them with one or combination of the tests listed above. If you read the manuscript by Aisbett, Lakens, and Sainani (2020) you will see this approach is logical and fairly straight forward. But, I imagine many former MBI are unsure how to accomplish this analysis since (1) this usually is not included in typical statistics education and (2) most have relied upon Hopkins’ spreadsheets to automatically perform the necessary calculations. I understand that many sport and exercise scientists do not have the requisite programming experience in SAS and R to feel comfortable with completing these analyses. In my opinion, it is worth the time to learn at least one of these programming languages, but if demand is great enough I will make a spreadsheet and post it to a repository that facilitates version control (e.g., GitHub).

Figure 1. Comparison of hypothesis tests. The traditional nil-hypothesis tests (a) the null hypothesis that the effect is exactly equal to zero. The minimal effects test (b) tests against a null hypothesis of the true effect falling between the upper and lower equivalence bound, and the equivalence test (c) tests against the null hypothesis that the true effect is outside (greater or less than) the equivalence bound. Finally, the non-inferiority test (d) tests against the null hypothesis that the effect is at least as great as the bound (in one direction).

Application in R

First, you will need to have the appropriate R packages for these analyses. I prefer to use afex (Singmann et al. 2020) and emmeans (Lenth 2020) because I find both pacakges easy to use, but other packages or base R functions could be used for these analyses. If you Google “How do I, insert procedure here, in R” you will likely get a variety of helpful results. So, if the procedures below don’t fit you needs then I’m sure there are numerous other resources within R that will be helpful. I highly suggest searching stackoverflow for potential solutions. We will also use the tidyverse package (Wickham et al. 2019) to help manage the data and broom to produce some nice looking tables (Robinson and Hayes 2020).

#Load the emmeans and afex packages
library(afex)
library(emmeans)
library(tidyverse)
library(broom)

Data

Now we need some data to analyze. In R this is straight forward since there are preloaded datasets available. For SAS, I will simply export this data as a csv file then import it into SAS using PROC IMPORT.

#Simple Three-Group 
data("PlantGrowth")

#Factorial 
data("ToothGrowth")

PlantGrowth Dataset

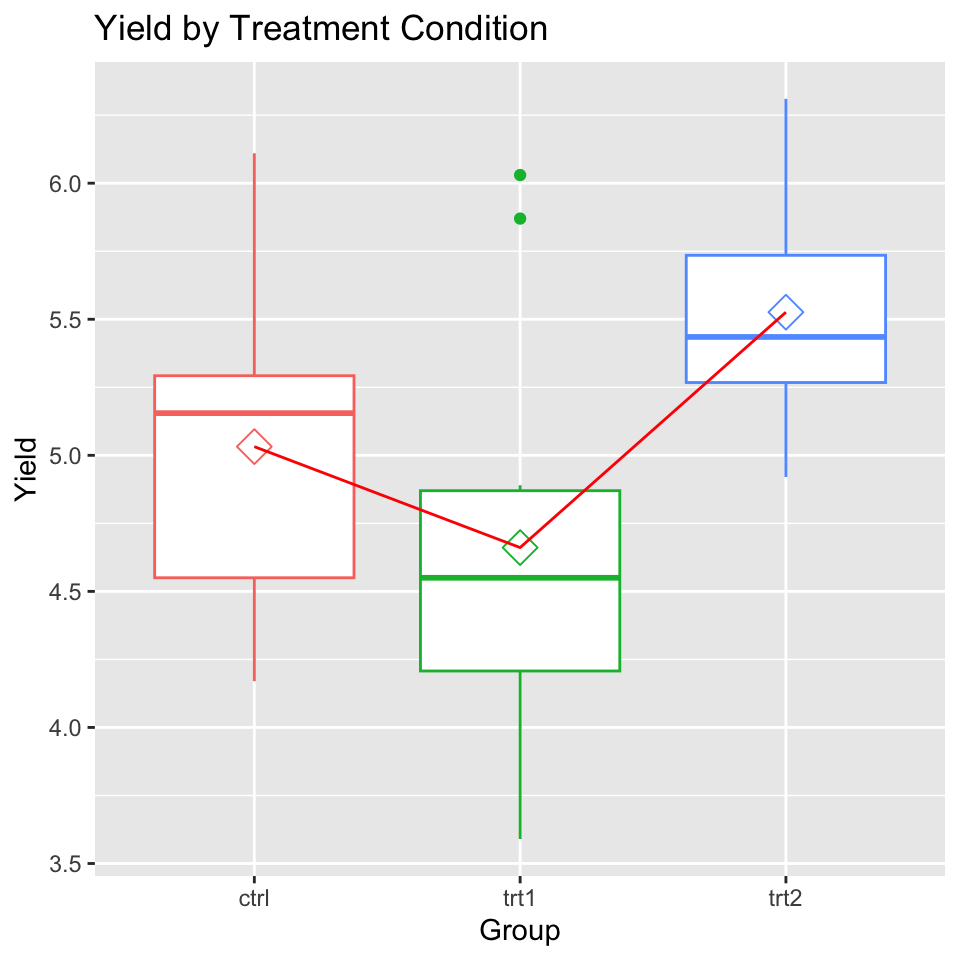
Figure 1: PlantGrowth Data Visualization.

Description:

“Results from an experiment to compare yields (as measured by dried weight of plants) obtained under a control and two different treatment conditions.”

head(PlantGrowth)

  weight group
1   4.17  ctrl
2   5.58  ctrl
3   5.18  ctrl
4   6.11  ctrl
5   4.50  ctrl
6   4.61  ctrl

ToothGrowth Dataset

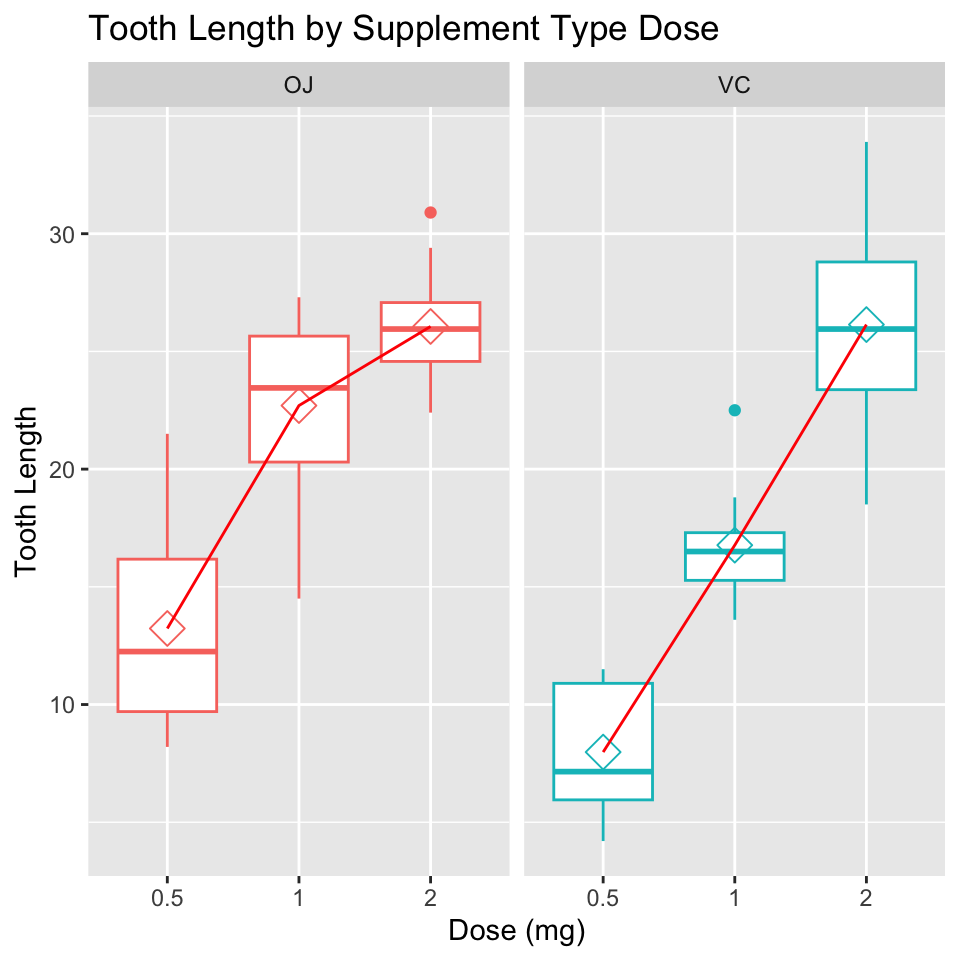
Figure 2: ToothGrowth Data Visualization.

Description:

“The response is the length of odontoblasts (cells responsible for tooth growth) in 60 guinea pigs. Each animal received one of three dose levels of vitamin C (0.5, 1, and 2 mg/day) by one of two delivery methods, orange juice or ascorbic acid (a form of vitamin C and coded as VC).”

head(ToothGrowth)

   len supp dose
1  4.2   VC  0.5
2 11.5   VC  0.5
3  7.3   VC  0.5
4  5.8   VC  0.5
5  6.4   VC  0.5
6 10.0   VC  0.5

Analysis of PlantGrowth

We will first have to add an “id” column to the PlantGrowth dataset and then build the ANOVA model using afex. In this scenario, we will consider a difference of 1 unit of weight to be the SESOI.

PlantGrowth = PlantGrowth %>% 
  dplyr::mutate(id = rownames(PlantGrowth)) 
mod_plantgrowth = afex::aov_car(weight ~ group + Error(id), 
                                data = PlantGrowth)

Contrasts set to contr.sum for the following variables: group

tidyaov_plantgrowth = broom::tidy(mod_plantgrowth$aov)
knitr::kable(tidyaov_plantgrowth)

Now, that we have a linear model this can be passed onto the emmeans package for equivalence and minimal effects testing.

Mechanistic (Equivalence-MET) Analysis

emm_plants = emmeans(mod_plantgrowth, trt.vs.ctrl1 ~ group, 
                     adjust = "none") 
# Sets one group as the control to compare against the treatments

# Note that adjust has to be set to "none" 
# otherwise the dunnett correction is applied
knitr::kable(confint(emm_plants$contrasts, level = .9), 
             caption = "Pairwise Comparisons with 90% C.I.")

Pairwise Comparisons with 90% C.I.
contrast	estimate	SE	df	lower.CL	upper.CL
trt1 - ctrl	-0.371	0.2787816	27	-0.8458455	0.1038455
trt2 - ctrl	0.494	0.2787816	27	0.0191545	0.9688455

#Equivalence Test
emm_equivalence = test(emm_plants, 
                       delta = 1, adjust = "none")
knitr::kable(emm_equivalence$contrasts, 
             caption = "Equivalence Tests")

Equivalence Tests
contrast	estimate	SE	df	t.ratio	p.value
trt1 - ctrl	-0.371	0.2787816	27	-2.256246	0.0161798
trt2 - ctrl	0.494	0.2787816	27	-1.815041	0.0403211

If we check the 90% confidence intervals, we can see that the upper limit (UL) is lower than the upper equivalence bound, but greater than the lower limit (LL) of the equivalence bound indicating equivalence at an alpha of .05 at both bounds. Pairwise comparisons indicate that both treatments are statistically equivalent (at least at our prespecified SESOI; delta parameter in the test function). Notice that only 1 p-value is reported, emmeans completes equivalence testing by taking the absolute difference between groups.

Equation `emmeans` appears to be using for equivalence testing:

$$t = \frac{|M_{1}-M_{2}|-\delta}{SEM}$.png$

Where M₁ and M₂ represent the means in condition 1 and condition 2 respectively, and $$\delta$.png$ represents a symmetrical equivalence bound, and SEM is the standard error of the mean.

Also, this is a one-tailed t-test:

$$p = Pr(T_{crit} < t)$.png$

Not a two-tailed test:

$$p = 2 \cdot Pr(T_{crit} > |t|)$.png$

While it is unnecessary given the equivalence tests results, let’s see how we could perform the METs in both directions (positive and negative).

#Minimal Effects Test: Positive
emm_MET = test(emm_plants, null = 1, 
               adjust = "none", side = ">")
knitr::kable(emm_MET$contrasts, 
             caption = "Minimal Effects Test: Positive")

Minimal Effects Test: Positive
contrast	estimate	SE	df	null	t.ratio	p.value
trt1 - ctrl	-0.371	0.2787816	27	1	-4.917828	0.9999810
trt2 - ctrl	0.494	0.2787816	27	1	-1.815041	0.9596789

#Minimal Effects Test: Negative
emm_MET = test(emm_plants, null = -1, adjust = "none", side = "<")
knitr::kable(emm_MET$contrasts, 
             caption = "Minimal Effects Test: Negative")

Minimal Effects Test: Negative
contrast	estimate	SE	df	null	t.ratio	p.value
trt1 - ctrl	-0.371	0.2787816	27	-1	2.256246	0.9838202
trt2 - ctrl	0.494	0.2787816	27	-1	5.359034	0.9999942

The conclusions from a “mechanistic” inference: Both treatments, compared to control, are moderately compatible with equivalence

Clinical (MET & Non-Inferiority Analysis)

The data can also be interpreted with the “clinical MBI” approach which essentially boils down to a strict (low alpha; default = .005) and a more lax MET for benefit (high alpha; default = .25). In any case, individual researchers should set the alpha-level a priori and justify this decision (Daniel Lakens et al. 2018; “Justify Your Alpha by Minimizing or Balancing Error Rate,” n.d.).

For simplicity let’s keep the defaults for this analysis.

First, we need to perform the non-inferiority tests. Luckily this is easy with emmeans.

#Non-Inferiority Test
emm_nonif = test(emm_plants, delta = 1, 
                 adjust = "none", 
                 side = "noninferiority")
knitr::kable(emm_nonif$contrasts, 
             caption = "Clinical Non-Inferiority")

Clinical Non-Inferiority
contrast	estimate	SE	df	t.ratio	p.value
trt1 - ctrl	-0.371	0.2787816	27	2.256246	0.0161798
trt2 - ctrl	0.494	0.2787816	27	5.359034	0.0000058

Treatment 1 (trt1) is only moderately compatible (given our predetermined alpha) with non-inferiority, but treatment 2 is strongly compatible (p < .005) with non-inferiority.

Now we can perform a MET for the benefit, but notice how the use of the test function has changed. Now, we call the null and side parameters to set the threshold and direction of the statistical test. In this case we can keep null as the same value since we are testing a positive effect and side is set to “>” to indicate we are testing for superiority.

#Minimal Effects Test
emm_nonif = test(emm_plants, null = 1, 
                 adjust = "none", side = ">")
knitr::kable(emm_nonif$contrasts, 
             caption = "Clinical MET")

Clinical MET
contrast	estimate	SE	df	null	t.ratio	p.value
trt1 - ctrl	-0.371	0.2787816	27	1	-4.917828	0.9999810
trt2 - ctrl	0.494	0.2787816	27	1	-1.815041	0.9596789

Conclusion: Do not use trt1 because we cannot assume non-inferiority. However, we can use trt2, which is compatible with non-inferiority, despite no evidence of any meaningful benefit.

Analysis of ToothGrowth Data

Again, we will need to add an “id” column to the ToothGrowth dataset and then build the ANOVA model using afex. Notice this time there is a interaction in the ANOVA. Also, in this case, we believe a difference of 3 units in len to be the SESOI.

ToothGrowth = ToothGrowth %>% 
  dplyr::mutate(id = rownames(ToothGrowth)) 
mod_Toothgrowth = afex::aov_car(len ~ supp*dose + Error(id),
                                data = ToothGrowth)

Converting to factor: dose

Contrasts set to contr.sum for the following variables: supp, dose

tidyaov_Toothgrowth = broom::tidy(mod_Toothgrowth$aov)

knitr::kable(tidyaov_Toothgrowth)

Now that we have a linear model this can be passed onto the emmeans package for equivalence and minimal effects testing.

Mechanistic (Equivalence-MET) Analysis

Compare Dosage

First, we want to compare Vitamin C dosage within each delivery method (VC or OJ) to see its effect on tooth growth.

emm_Tooths = emmeans(mod_Toothgrowth, 
                     revpairwise ~ dose|supp, 
                     adjust = "none") 
# Pairwise comparisions within each treatment across dosages

# Note that adjust has to be set to "none" 
# otherwise the dunnett correction is applied
knitr::kable(confint(emm_Tooths$contrasts, level = .9), 
             caption = "Pairwise Comparisons with 90% C.I.")

Pairwise Comparisons with 90% C.I.
contrast	supp	estimate	SE	df	lower.CL	upper.CL
dose1 - dose0.5	OJ	9.47	1.624016	54	6.752103	12.187897
dose2 - dose0.5	OJ	12.83	1.624016	54	10.112103	15.547897
dose2 - dose1	OJ	3.36	1.624016	54	0.642103	6.077897
dose1 - dose0.5	VC	8.79	1.624016	54	6.072103	11.507897
dose2 - dose0.5	VC	18.16	1.624016	54	15.442103	20.877897
dose2 - dose1	VC	9.37	1.624016	54	6.652103	12.087897

#Equivalence Test
emm_equivalence = test(emm_Tooths, 
                       delta = 3, adjust = "none")
knitr::kable(emm_equivalence$contrasts, 
             caption = "Equivalence Tests")

Equivalence Tests
contrast	supp	estimate	SE	df	t.ratio	p.value
dose1 - dose0.5	OJ	9.47	1.624016	54	3.9839496	0.9998977
dose2 - dose0.5	OJ	12.83	1.624016	54	6.0528941	0.9999999
dose2 - dose1	OJ	3.36	1.624016	54	0.2216726	0.5872975
dose1 - dose0.5	VC	8.79	1.624016	54	3.5652347	0.9996148
dose2 - dose0.5	VC	18.16	1.624016	54	9.3348805	1.0000000
dose2 - dose1	VC	9.37	1.624016	54	3.9223739	0.9998752

If we check the 90% confidence intervals, we can see that the lower limit (LL) is higher than the upper equivalence bound, in all but one condition, indicating non-equivalence at an alpha of .05 at both bounds. Pairwise comparisons indicate that none of the doses in either treatment can be considered equivalent.

Now, let’s perform the METs in both directions (positive and negative).

#Minimal Effects Test: Positive
emm_MET = test(emm_Tooths, null = 3, 
               adjust = "none", side = ">")
knitr::kable(emm_MET$contrasts, 
             caption = "Minimal Effects Test: Positive")

Minimal Effects Test: Positive
contrast	supp	estimate	SE	df	null	t.ratio	p.value
dose1 - dose0.5	OJ	9.47	1.624016	54	3	3.9839496	0.0001023
dose2 - dose0.5	OJ	12.83	1.624016	54	3	6.0528941	0.0000001
dose2 - dose1	OJ	3.36	1.624016	54	3	0.2216726	0.4127025
dose1 - dose0.5	VC	8.79	1.624016	54	3	3.5652347	0.0003852
dose2 - dose0.5	VC	18.16	1.624016	54	3	9.3348805	0.0000000
dose2 - dose1	VC	9.37	1.624016	54	3	3.9223739	0.0001248

#Minimal Effects Test: Negative
emm_MET = test(emm_Tooths, null = -3, 
               adjust = "none", side = "<")
knitr::kable(emm_MET$contrasts, 
             caption = "Minimal Effects Test: Negative")

Minimal Effects Test: Negative
contrast	supp	estimate	SE	df	null	t.ratio	p.value
dose1 - dose0.5	OJ	9.47	1.624016	54	-3	7.678493	1.0000000
dose2 - dose0.5	OJ	12.83	1.624016	54	-3	9.747438	1.0000000
dose2 - dose1	OJ	3.36	1.624016	54	-3	3.916216	0.9998727
dose1 - dose0.5	VC	8.79	1.624016	54	-3	7.259778	1.0000000
dose2 - dose0.5	VC	18.16	1.624016	54	-3	13.029424	1.0000000
dose2 - dose1	VC	9.37	1.624016	54	-3	7.616918	1.0000000

We see that the data, in almost all conditions, is highly compatible with the hypothesis that a higher dosage results in a meaningful positive effect. However, it is inconclusive (non-equivalent and non-positive) if increasing dosage with OJ to 2 from 1 improves tooth growth.

The conclusions from a “mechanistic” inference: Increasing dosage of OJ or VC results in increased tooth growth, but it is inconclusive if increasing OJ dosage (from 1 to 2) results in a meaningful improvement.

Compare Delivery Methods

You may want to compare each delivery method at the specified doses. To do so, you simply flip the order of the factors in emmeans.

emm_Tooths = emmeans(mod_Toothgrowth, 
                     revpairwise ~ supp|dose, 
                     adjust = "none") 

knitr::kable(confint(emm_Tooths$contrasts, level = .9), 
             caption = "Pairwise Comparisons with 90% C.I.")

Pairwise Comparisons with 90% C.I.
contrast	dose	estimate	SE	df	lower.CL	upper.CL
VC - OJ	0.5	-5.25	1.624016	54	-7.967897	-2.532103
VC - OJ	1	-5.93	1.624016	54	-8.647897	-3.212103
VC - OJ	2	0.08	1.624016	54	-2.637897	2.797897

#Equivalence Test
emm_equivalence = test(emm_Tooths, 
                       delta = 3, adjust = "none")
knitr::kable(emm_equivalence$contrasts, 
             caption = "Equivalence Tests")

Equivalence Tests
contrast	dose	estimate	SE	df	t.ratio	p.value
VC - OJ	0.5	-5.25	1.624016	54	1.385454	0.9141950
VC - OJ	1	-5.93	1.624016	54	1.804169	0.9616084
VC - OJ	2	0.08	1.624016	54	-1.798011	0.0388832

#Minimal Effects Test: Positive
emm_MET = test(emm_Tooths, null = 3, 
               adjust = "none", side = ">")
knitr::kable(emm_MET$contrasts, 
             caption = "Minimal Effects Test: Positive")

Minimal Effects Test: Positive
contrast	dose	estimate	SE	df	null	t.ratio	p.value
VC - OJ	0.5	-5.25	1.624016	54	3	-5.079998	0.9999976
VC - OJ	1	-5.93	1.624016	54	3	-5.498713	0.9999995
VC - OJ	2	0.08	1.624016	54	3	-1.798011	0.9611168

#Minimal Effects Test: Negative
emm_MET = test(emm_Tooths, null = -3, 
               adjust = "none", side = "<")
knitr::kable(emm_MET$contrasts, 
             caption = "Minimal Effects Test: Negative")

Minimal Effects Test: Negative
contrast	dose	estimate	SE	df	null	t.ratio	p.value
VC - OJ	0.5	-5.25	1.624016	54	-3	-1.385454	0.0858050
VC - OJ	1	-5.93	1.624016	54	-3	-1.804169	0.0383916
VC - OJ	2	0.08	1.624016	54	-3	1.896532	0.9683779

Conclusion: the data is weakly compatible with a negative effect of VC at the lower 2 doses, but is moderately compatible with equivalence at the highest dosage.

Clinical (MET & Non-Inferiority Analysis)

For the “clinical MBI” approach let’s again use the same alphas as before (non-inferiority: .005 and MET: .25)

For simplicity, let’s just compare the delivery methods at each dosage.

#Non-Inferiority Test
emm_nonif = test(emm_Tooths, delta = 3, 
                 adjust = "none", 
                 side = "noninferiority")
knitr::kable(emm_nonif$contrasts, 
             caption = "Clinical Non-Inferiority")

Clinical Non-Inferiority
contrast	dose	estimate	SE	df	t.ratio	p.value
VC - OJ	0.5	-5.25	1.624016	54	-1.385454	0.9141950
VC - OJ	1	-5.93	1.624016	54	-1.804169	0.9616084
VC - OJ	2	0.08	1.624016	54	1.896532	0.0316221

#Minimal Effects Test
emm_nonif = test(emm_Tooths, null = 3, 
                 adjust = "none", side = ">")
knitr::kable(emm_nonif$contrasts, 
             caption = "Clinical MET")

Clinical MET
contrast	dose	estimate	SE	df	null	t.ratio	p.value
VC - OJ	0.5	-5.25	1.624016	54	3	-5.079998	0.9999976
VC - OJ	1	-5.93	1.624016	54	3	-5.498713	0.9999995
VC - OJ	2	0.08	1.624016	54	3	-1.798011	0.9611168

In this case, VC fails to adequately demonstrate non-inferiority.

Conclusion: Do not use VC at any dosage as it does not demonstrate adequate non-inferiority to OJ, and failed to provide any evidence of having a meaningful positive effect.

Application in SAS

For the most part this will be accomplished using SAS’s PROC MIXED, but a number of procedures also support these functions (Kiernan et al. 2011). The only SAS procedure I would suggest not using is PROC GLM, as I do not believe SAS has done anything to update this procedure in quite some time. I see no advantage of using PROC GLM over PROC MIXED. For simplicity, I will only being doing one analysis for each dataset.

Import Data

First, you will need to export the data from R.

write.csv(ToothGrowth, "tooth.csv")

write.csv(PlantGrowth, "plant.csv")

Now, we can import it into SAS with PROC IMPORT. Remember, to change the file path!

PROC IMPORT OUT= WORK.plant 
            DATAFILE= "C:\Users\aaron.caldwell\Documents\plant.csv" 
            DBMS=CSV REPLACE;
     GETNAMES=YES;
     DATAROW=2; 
RUN;

PROC IMPORT OUT= WORK.tooth 
            DATAFILE= "C:\Users\aaron.caldwell\Documents\tooth.csv" 
            DBMS=CSV REPLACE;
     GETNAMES=YES;
     DATAROW=2; 
RUN;

Analysis of PlantGrowth – Mechanistic (Equivalence-MET) Analysis

In this scenario, we will consider a difference of 1 unit of weight to be the SESOI.

Now, in SAS’s PROC MIXED equivalence and minimal effects testing will be carried out via the LSMESTIMATE statement.


/*Mechanistic MBI */
title "Mechanistic MBI: PlantGrowth";
PROC MIXED data=plant;
class group;
model weight = group;
lsmeans group / CL; /*Gets all the means and CI for each condition*/
lsmestimate group
"ctrl v trt1" [1, 1] [-1,2], /*The first number sets the contrast and the assigns the level of group*/
"ctrl v trt2" [1, 1] [-1,3]
/ TESTVALUE=-1 UPPER CL; /*Lower bound equivalence test*/
lsmestimate group
"ctrl v trt1" [1, 1] [-1,2],
"ctrl v trt2" [1, 1] [-1,3]
/ TESTVALUE=1 LOWER CL; /*Upper bound equivalence test*/
run;
quit;

Figure 2. LSMESTIMATE Results for Equivalence Testing on Plant Data.

If we check the confidence limits, we can see that the upper limit (UL) is lower than the upper equivalence bound, but greater than the lower limit (LL) of the equivalence bound indicating equivalence at an alpha of .05 at both bounds. Pairwise comparisons indicate that both treatments are statistically equivalent (at least at our prespecified SESOI set by the TESTVALUE parameter in the LSMESTIMATE statement). Notice that only 2 p-values are reported, unlike emmeans we must perform an upper bound and lower bound test. We only infer equivalence if the highest p-value for each comparison is less than the predetermined alpha.

The conclusions from a “mechanistic” inference: Both treatments, compared to control, are moderately compatible with equivalence

ToothGrowth Clinical (MET & Non-Inferiority) Analysis

This is fairly straight forward in SAS. All we need to do is modify the upper bound TESTVALUE and modify the alpha. For the “clinical MBI” approach let’s change the alpha for the MET (non-inferiority: .005 and MET: .2).

/*Clinical MBI */
title "Clinical MBI: ToothGrowth";
PROC MIXED data=tooth;
class supp dose;
model len = supp|dose;
lsmeans supp*dose / CL;  /*Gets all the means and CI for each condition*/
lsmestimate supp*dose
"OJ vs VC @ 0.5 mg dose" [-1, 1 3] [1, 2 3],
"OJ vs VC @ 1 mg dose" [-1, 1 1] [1, 2 1],
"OJ vs VC @ 2 mg dose" [-1, 1 2] [1, 2 2]
/ TESTVALUE=-1 CL UPPER alpha=.005;
lsmestimate supp*dose
"OJ vs VC @ 0.5 mg dose" [-1, 1 3] [1, 2 3],
"OJ vs VC @ 1 mg dose" [-1, 1 1] [1, 2 1],
"OJ vs VC @ 2 mg dose" [-1, 1 2] [1, 2 2]
/ TESTVALUE=1 CL UPPER alpha=.2;
run;
quit;

For simplicity, let’s just compare the delivery methods at each dosage.

Figure 3. LSMESTIMATE Results for Equivalence Testing on Tooth Data.

In this case, VC fails to adequately demonstrate non-inferiority.

Conclusion: Do not use VC at any dosage as it does not demonstrate adequate non-inferiority to OJ, and failed to provide any evidence of having a meaningful positive effect.

Writing your Methods

One of the more frustrating problems I noticed with research reporting MBI in the past was the lack of detail in their methods sections about the statistical methods they utilized. Frankly this is a problem in most sport and exercise science manuscripts, not just those that utilized MBI. Therefore, I have created a short list of items that should always be included if you are using this approach.

Note what types of hypotheses you are testing.

If you are using the “mechanistic” approach: note that you are simply performing an equivalence/MET test
If you are using the “clincal” approach: note that you are using a non-inferiority test and a minimal effects test

State the alpha level(s)

Even if you are using the “compatibility” bounds outlined by Aisbett, Lakens, and Sainani (2020) you should directly state the alpha levels for used within your manuscript.
Justifying your alpha can be difficult and should be done a priori. Most likely, this can be accomplished when you are planning your sample size for data collection by balancing your type 1 and type 2 error using a compromise power analysis.
- There are blog posts from minitab and Lakens that may be helpful here.

State your smallest effect size(s) of interest (SESOI)

In most cases of MBI users have defaulted to a difference of 0.2 standard deviations (Cohen’s d = 0.2)
I would encourage researchers to have justification for their SESOI whether based on practitioner preferences (e.g., “coaches have stated an interest in an effect of X magnitude”) or based on empirical evidence. -For empirical justifications, I suggest reading the DETLA2 guidelines (Cook et al. 2018).

Note and cite what statistical software and programs you used to analyze the data.

Try to be specific and include version number
- This is important because as the software is updated some calculations may change.

Concluding Remarks

Any researcher is capable of performing the appropriate equivalence, MET, and non-inferiority tests in R or SAS. As I have documented, making a “magnitude based inference” is fairly simple and straight forward procedure when it is viewed through these lenses. All of these approaches (equivalence, MET, and non-inferiority tests) in the scenarios I have outlined are special cases of a one-tailed t-test. Researchers who would like to adopt this approach should read the work by Aisbett, Lakens, and Sainani (2020) to ensure they fully understand the statistical framework. Both Batterham & Hopkins, the creators of MBI, should be also commended for moving the conversation surrounding statistical inference in sport science from a focus on “nil hypotheses” to a focus on the magnitude of the effect size. However, I would strongly encourage all sports scientists that have used magnitude based inference in the past to adopt this straightforward frequentist approach or adopt a fully Bayesian approach to inference (Ravenzwaaij et al. 2019).

Questions?

If you have any questions, please feel free to contact me.

References

Aisbett, Janet, Daniel Lakens, and Kristin Sainani. 2020. “Magnitude Based Inference in Relation to One-Sided Hypotheses Testing Procedures,” May. https://doi.org/10.31236/osf.io/pn9s3.

Amrhein, Valentin, David Trafimow, and Sander Greenland. 2019. “Inferential Statistics as Descriptive Statistics: There Is No Replication Crisis If We Don’t Expect Replication.” The American Statistician 73 (sup1): 262–70. https://doi.org/10.1080/00031305.2018.1543137.

Batterham, Alan M., and William G. Hopkins. 2006. “Making Meaningful Inferences about Magnitudes.” International Journal of Sports Physiology and Performance 1 (1): 50–57. https://doi.org/10.1123/ijspp.1.1.50.

Chow, Zad R., and Sander Greenland. 2019. “Semantic and Cognitive Tools to Aid Statistical Inference: Replace Confidence and Significance by Compatibility and Surprise.” https://arxiv.org/abs/1909.08579.

Cook, Jonathan A., Steven A. Julious, William Sones, Lisa V. Hampson, Catherine Hewitt, Jesse A. Berlin, Deborah Ashby, et al. 2018. “Choosing the Target Difference (&Ldquo$\mathsemicolon$effect Size&rdquo$\mathsemicolon$) for a Randomised Controlled Trial - DELTA$\less$sup$\greater$2$\less$/Sup$\greater$&nbsp$\mathsemicolon$guidance,” August. https://doi.org/10.20944/preprints201808.0521.v1.

Greenland, Sander, and Zad R. Chow. 2019. “To Aid Statistical Inference, Emphasize Unconditional Descriptions of Statistics.” https://arxiv.org/abs/1909.08583.

“Justify Your Alpha by Minimizing or Balancing Error Rate.” n.d. http://http://daniellakens.blogspot.com/2019/05/justifying-your-alpha-by-minimizing-or.html.

Kiernan, Kathleen, Randy Tobias, Phil Gibbs, and Jill Tao. 2011. “CONTRAST and ESTIMATE Statements Made Easy: The LSMESTIMATE Statement.” SAS Global Forum 2011 (351): 1–19. https://support.sas.com/resources/papers/proceedings11/351-2011.pdf.

Lakens, Daniel, Federico G. Adolfi, Casper J. Albers, Farid Anvari, Matthew A. J. Apps, Shlomo E. Argamon, Thom Baguley, et al. 2018. “Justify Your Alpha.” Nature Human Behaviour 2 (3): 168–71. https://doi.org/10.1038/s41562-018-0311-x.

Lakens, Daniël, Anne M. Scheel, and Peder M. Isager. 2018b. “Equivalence Testing for Psychological Research: A Tutorial.” Advances in Methods and Practices in Psychological Science 1 (2): 259–69. https://doi.org/10.1177/2515245918770963.

———. 2018a. “Equivalence Testing for Psychological Research: A Tutorial.” Advances in Methods and Practices in Psychological Science 1 (2): 259–69. https://doi.org/10.1177/2515245918770963.

Lenth, Russell. 2020. Emmeans: Estimated Marginal Means, Aka Least-Squares Means. https://CRAN.R-project.org/package=emmeans.

Lohse, Keith, Kristin Sainani, J. Andrew Taylor, Michael Lloyd Butson, Emma Knight, and Andrew Vickers. 2020. “Systematic Review of the Use of ‘Magnitude-Based Inference’ in Sports Science and Medicine.” Center for Open Science. https://doi.org/10.31236/osf.io/wugcr.

Peterson, Kyle, and Aaron Caldwell. 2019. Mbir: Magnitude-Based Inferences. https://CRAN.R-project.org/package=mbir.

Rafi, Zad, and Andrew D. Vigotsky. 2020. concurve: Computes and Plots Compatibility (Confidence) Intervals, p-Values, s-Values, & Likelihood Intervals to Form Consonance, Surprisal, & Likelihood Functions. https://CRAN.R-project.org/package=concurve.

Ravenzwaaij, Don van, Rei Monden, Jorge N. Tendeiro, and John P. A. Ioannidis. 2019. “Bayes Factors for Superiority, Non-Inferiority, and Equivalence Designs.” BMC Medical Research Methodology 19 (1). https://doi.org/10.1186/s12874-019-0699-7.

Robinson, David, and Alex Hayes. 2020. Broom: Convert Statistical Analysis Objects into Tidy Tibbles. https://CRAN.R-project.org/package=broom.

Sainani, Krisitin. 2018. “The Problem with ‘Magnitude-Based Inference’.” Medicine & Science in Sports & Exercise 50 (10): 2166–76. https://doi.org/10.1249/mss.0000000000001645.

Sainani, Kristin L., Keith R. Lohse, Paul Remy Jones, and Andrew Vickers. 2019. “Magnitude-Based Inference Is Not Bayesian and Is Not a Valid Method of Inference.” Scandinavian Journal of Medicine & Science in Sports 29 (9): 1428–36. https://doi.org/10.1111/sms.13491.

Singmann, Henrik, Ben Bolker, Jake Westfall, Frederik Aust, and Mattan S. Ben-Shachar. 2020. Afex: Analysis of Factorial Experiments. https://CRAN.R-project.org/package=afex.

Wickham, Hadley, Mara Averick, Jennifer Bryan, Winston Chang, Lucy D’Agostino McGowan, Romain François, Garrett Grolemund, et al. 2019. “Welcome to the tidyverse.” Journal of Open Source Software 4 (43): 1686. https://doi.org/10.21105/joss.01686.

Introduction

Note of caution

The Basic Concepts

Terminology

Application in R

Data

PlantGrowth Dataset

ToothGrowth Dataset

Analysis of PlantGrowth

Mechanistic (Equivalence-MET) Analysis

Equation emmeans appears to be using for equivalence testing:

Clinical (MET & Non-Inferiority Analysis)

Analysis of ToothGrowth Data

Mechanistic (Equivalence-MET) Analysis

Clinical (MET & Non-Inferiority Analysis)

Application in SAS

Import Data

Analysis of PlantGrowth – Mechanistic (Equivalence-MET) Analysis

ToothGrowth Clinical (MET & Non-Inferiority) Analysis

Writing your Methods

Concluding Remarks

Questions?

References

Equation `emmeans` appears to be using for equivalence testing: